|
|
|
DESPRE SPECTREGheorghe Oproescu - Tavi YO4BKM
William Thomson (lord Kelvin, 1824-1906) protesta, la
sfârşitul sec. XIX, cu ocazia intenţiei de a se scoate obiectul “Logică” din
şcoli pentru a face loc altor discipline ale ştiinţei moderne, spunând: “Niciun
comandant de navă nu poate fi acuzat că nu cunoaşte bine navigaţia pe mări şi
oceane. Ceea ce duce însă la naufragii este necunoaşterea logicii care leagă
observaţia practică de intimitatea fenomenelor observate”. Industria de azi oferă la gata
orice este nevoie pentru satisfacerea pasiunii noastre: kituri mai mult sau mai
puţin complete, aparate gata reglate pentru orice situaţie, softuri de trafic,
de depanare, de control şi reglare, dar care ne îndepărtează tot mai mult de
miezul lucrurilor. Prin 1975 am văzut la radioclubul judeţean Argeş un dosar cu
lucrări scrise ale radioamatorilor la examenele de certificare susţinute cu ani
în urmă. Printre cele care mi-au rămas în memorie se afla una cu subiectul
“Multiplicarea de frecvenţă” în care se trata, pe mai multe pagini, o întreagă
teorie a semnalelor cuprinzând forme, distorsionări şi spectrul de armonice. I-am
dat atenţie deoarece cu multi ani în urmă citeam în “Sport şi Tehnică” un
excelent serial de articole pe această temă şi simţeam că mă depăşeşte, deşi
formalismul fizic şi matematic îmi era foarte familiar
prin natura pregătirii mele de specialitate. Atunci mi-am dat seama că
radioamatorismul nu este deloc amatorism şi este bine să fie luat de la fundamente,
indiferent ce profesie ai avea. Când am început să-mi fac echipamentele pe 144
MHz, după scheme proprii, adaptate la piesele pe care le aveam şi am avut de
făcut inclusiv multiplicări de frecvenţă, am văzut la modul concret ce înseamnă
să realizezi distorsiunea optimă a undei sinusoidale pentru a avea maximum de
energie pe armonica dorită. Şi nu eram singurul care îşi executa
echipamentele singur, în clubul argeşean mai erau cel puţin o duzină. Dar,
după mai bine de 40 de ani, a devenit accesibil şi comod să ai totul la gata.
Cu dezavantajul de a nu mai avea posibilitatea să evaluezi performanţele
acestor echipamente folosind alte căi decât tot pe cele oferite de furnizor,
pentru că nu mai ai nici timpul, nici resursele să înţelegi cum, nu ce
face achiziţia în care ai investit doar bani. Timpul prea scurt într-o eră prea
alertă sau cine ştie ce alte interese tot “fură” sau duc în necunoaştere intimitatea
fenomenelor observate iar noi devenim tributarii unor analize făcute de alţii,
care au programat nu numai cum să funcţioneze echipamentele prevăzute cu
inteligenţă artificială, dar au programat în ele inclusiv ipoteze proprii, de
multe ori neprecizate. Am întâlnit aplicaţii tip soft pentru analiza multor
tipuri de circuite, de la filtre la antene şi am constatat cu uimire că grafice
cu asimptote erau rezolvate în formă continuă, cu valori finite pe tot
domeniul. Am înţeles greşeala, programatorul a fost comod când a rezolvat
asimptota (destul de migălos şi cere ceva fantezie) şi, pur şi simplu, a
programat ca mărimilor care depăşesc o anumită limită să li se atribuie valori
finite pentru a nu avea probleme cu scalarea graficelor. Dacă nu aş fi cunoscut
că fenomenul descris de aplicaţie are discontinuităţi, aş fi tras multe
concluzii greşite. De aceea cele ce urmează reprezintă o pledoarie pro domo
a tainelor din spectre. O fac fără să dezvolt vreun aparat matematic care ar
putea îngreuna înţelesul, dar pe care l-am folosit la construirea exemplelor cu
care voi susţine prezentarea. Înainte de a intra în detalii, fac o precizare: convenţional
au existat două categorii de spectre, spectre cu componente discrete (seria
Fourier) şi spectre continui (transformata Fourier). La care, de ani buni, s-a
mai adăugat încă una: spectrele semnalelor eşantionate, care s-a separat din
spectrele continui, dar formează deja o categorie distinctă. 1.
Spectrele seriei Fourier.
Acestea se folosesc numai la semnalele strict
periodice pe toată durata lor, care au o pulsaţie (frecvenţă) de bază numită
pulsaţie (frecvenţă) fundamentală, w0.
Sunt cele mai cunoscute şi, poate de aceea, tind să ţină locul oricăror alte
tipuri de spectre, conducând la erori dacă nu sunt folosite în deplină
cunoştinţă de cauză.
Ceea ce se numeşte serie Fourier este un şir infinit de termeni
creat artificial cu scopul de a compune orice formă de semnal periodic, nu
de a descrie spectrul real al semnalului. Fiecare termen reprezintă o
componentă pur armonică (de formă sinusoidală, cu amplitudinea şi faza iniţială
strict constante),
- Un semnal pur sinusoidal (semnal
armonic) are ca armonică numai pe el însuşi (armonica de ordinul 1), celelalte armonice
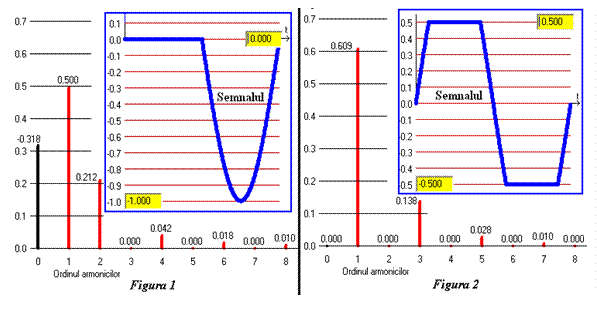
au amplitudini nule; - Un semnal asimetric are numai
armonice pare, figura 1; - Un semnal simetric are numai
armonice impare, figura 2; - Spectrul nu depinde de durata
semnalului în timp. Cele arătate mai sus au multiple
utilizări în special în domeniul sintezei semanlelor periodice nearmonice, dar
se folosesc şi la dimensionarea multiplicatoarelor de frecvenţă, pornind de la
o frecvenţă de bază a unui semnal armonic care este distorsionat prin limitări
superioare şi inferioare. Pentru a obţine eficienţă maximă la multiplicare semnalul
trebuie distorsionat în mod diferit funcţie de armonica pe care o dorim să fie
maximă. În tabelul nr. 1 se prezintă nivelele limitărilor pe semialternanţele semnalului
de bază funcţie de ordinul armonicei, semnalul de bază având amplitudinea egală
cu 1, precum şi amplitudinea maximă ce poate fi atinsă pentru armonica dorită.
Aceste nivele de limitare se pot exprima fie ca procente din amplitudine, fie ca
unghiuri de fază între care există semnalul de bază,
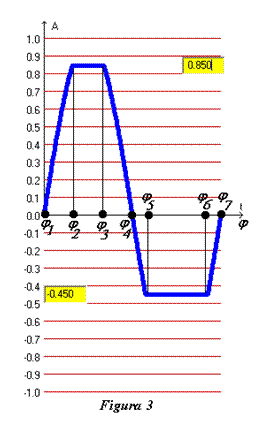
figura 3. O perioadă a semanlului întreg se întinde pe un unghi de fază cuprins
între 00 şi 3600, folosesc notaţiile în grade deoarece
sunt mai comune, în aplicaţii trebuie folosite valorile în radiani. În figura 3
semialternanţa superioară aparţine unei sinusoide între unghiurile de fază j1 şi j2 plus j3
şi j4 , între j1
şi j2 semnalul este limitat la o valoare constantă de 0,850 din amplitudinea iniţială. La fel stau lucrurile şi pentru
semialternanţa inferioară, limitarea fiind la valoarea de -0,450 din
amplitudinea iniţială. Ca exemplu concret, un nivel de 100% al unei semialternanţe
înseamnă că semanlul există între fazele 0---1800 dacă ne referim la
semialternanţa superioară sau între 1800-3600 dacă ne
referim la o semialternanţă inferioară, un nivel de 50% înseamnă un semnal
între fazele 00-300 plus 1500-1800
respectiv 1800- 2100 plus 3300-3600. Tabelul nr. 1. Limitările optime ale semnalului sinusoidal pentru diferite armonice Armonica nr. 2 3 4 5 6 7 Nivel
alternanţă superioară % 0% 50% 0% 30% 0% 20% faza - 00-300 1500-1800 - 00-17,50 162,50-1800 - 00-11,50 168,50-1800 Nivel
alternanţă inferioară % 100% 50% 70,7% 30% 50% 20% faza 1800-3600 1800- 2100 3300-3600 1800-2250 3150-3600 1800- 197,50 342,50-3600 1800- 2100 3300-3600 1800- 191,50 348,50-3600 Amplitudinea 0,212 0,138 0,072 0,050 0,034 0,026 Se
observă scăderea semnificativă a amplitudinii cu ordinului armonicei şi, poate
cel mai dezavantajos lucru, micşorarea unghiurilor de fază pentru care semnalul
trebuie să îşi păstreze forma sinusoidală, ceea face dificilă distorsionarea
lui corectă conform teoriei. La acestea se adaugă dificultatea separării armonicii
dorite prin filtrare de armonicele adiacente. De aceea nu se folosesc
multiplicări de frecvenţă mai mari de 3, uneori se ajunge la 5 şi, în situaţii
excepţionale la 10. Distorsionarea se face foarte simplu pentru armonica a doua,
folosind o diodă, pentru celelalte armonice sunt necesare componente active
polarizate corespunzător în raport cu nivelul semnalului supus distorsionării. Se mai pot folosi pentru
multiplicare de frecvenţă şi alte forme de semnal [2], în figura 4 se arată
spectrele semnalelor triunghiular şi dinte de ferăstrău. Semnalul triunghiular
admite o linie de simetrie şi generează numai armonice impare, semnalul dinte
de ferăstrău generează toate armonicele. La semnalul triunghiular armonica nr.
1 are amplitudinea de 81% din amplitudinea semnalului, la dintele de ferăstrău
această armonică are valoarea de 32%. Prin comparaţie grafică se poate deduce
şi amplitudinea celorlalte armonice. Spectrul semnalului dinte de ferăstrău
rămâne acelaşi şi dacă semnalul se deplasează deasupra sau dedesubtul axei
timpului deoarece rămâne simetric în raport cu el însuşi, apare în schimb
componenta de ordinul 0 care nu interesează. 2.
Spectrele continui. Spectrele continui apar la orice
fel de semnal, fie el periodic sau neperiodic. Evidenţierea lor se face cu
transformata Fourier, care este de fapt un operator matematic care transformă o
funcţie reală de timp (semnalul) într-o funcţie complexă, al cărei modul este
chiar spectrul şi se mai numeşte funcţie spectrală. Datorită dificultăţilor la
calcularea transformatei Fourier (o integrală improprie dintr-o funcţie de
variabile complexe) s-a propus o variantă simplificată, transformata Fourier
rapidă (TFR pe româneşte, FFT – fast Fourier transform – pe englezeşte) care
produce însă atât confuzii destul de mari la interpretarea spectrului cât şi
erori de determinare. Deşi tehnica de calcul de azi nu mai se împiedică în
calcularea prin transformata Fourier clasică, mulţi preferă să folosească TFR
deşi în lumea ştiinţifică sunt probate dezavantajele ei. Unele din ele le voi
arăta şi eu. Un
spectru continuu are componente armonice pentru orice pulsaţie (frecvenţă)
cuprinsă pe un domeniu continuu între 0 şi infinit, nu doar pentru anumite
frecvenţe discrete ca la seria Fourier. El se deosebeşte fundamental de
spectrul seriei Fourier deoarece depinde şi de durata semnalului. Pentru
semnale periodice spectrul continuu prezintă maxime în jurul frecvenţelor care
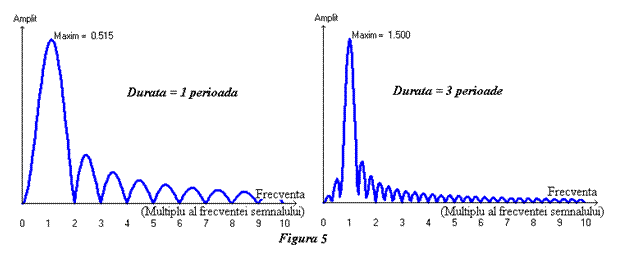
apar în spectrul discret dat de seria Fourier. Figura 5 arată spectrul continuu
al unui semnal pur sinusoidal cu amplitudinea egală cu 1, care durează o
perioadă (figura 5 stânga) sau trei perioade (figura 5
dreapta).
Conform seriei Fourier spectrul nu ar fi trebuit să aibe componente
armonice, din modul cum a fost concepută această serie nici nu au cum să apară,
în schimb transformata Fourier realizează o analiză completă a semnalului,
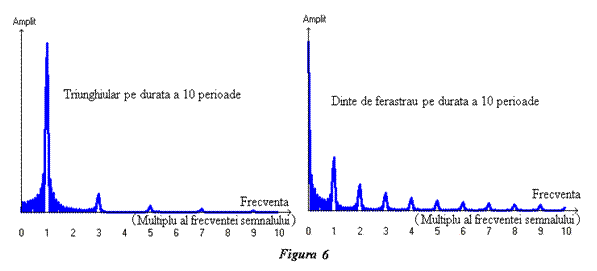
evidenţiind un spectru care caracetrizează distribuţia energiei în semnal. Figura
6 arată spectrul continuu al semnalelor pentru care figura 4 arată spectrul
discret. Cu creşterea duratei semnalului,
exprimată în număr de perioade, spectrul unui semnal pur armonic se grupează în
jurul pulsaţiei semnalului de bază iar amplitudinea creşte. Valoarea
amplitudinii din graficul spectrului nu are legătură cu amplitudinea
componentei spectrale ci aria mărginită de curba spectrală este o măsură a
distribuirii energiei din spectru pe diferite frecvenţe. Pentru un semnal sinusoidal
care durează infinit de mult spectrul devine o linie verticală fără grosime
aşezată pe pulsaţia fundamentală, cu amplitudinea infinită, dar care mărgineşte
o arie finită, cu valoarea 3,74.... indiferent frecvenţa şi amplitudinea
semnalului. Pentru cine este obişnuit cu asemenea cidăţenii poate că nu îi este
străină funcţia Dirac, cu aceleaşi proprietăţi, numai că aria mărginită de ea are
valoarea 1, deoarece este o funcţie construită artificial.
Ce am arătat mai sus este în schimb “găselniţa” mea [4], voi mai evidenţia şi
altele, cum ar fi aceea că restrâgerea spectrului cu creşterea duratei sale
respectă unul din principiile de incertitudine ale lui Heisenberg [3], dar fără
importanţă pentru ce urmează. Important este că din punct de vedere spectral
două semnale periodice sunt identice nu numai dacă au aceeaşi formă şi valori în
timp, ci şi durată. Semnalele neperiodice au şi ele spectre continui
care caracterizează fiecare tip de semnal şi îi determină ce se numeşte
amprenta semnalului. 3.
Spectrele semnalelor eşantionate. Am arătat că un semnal continuu
are un număr infinit de mare de componente spectrale cu pulsaţia distribuită pe
un domeniu continuu, fără “goluri”. Mai exact spus, pentru orice pulsaţie aleasă
în intervalul 0---infinit există o componentă armonică cu o amplitudine şi fază
iniţială bine precizate. Numai că acest lucru este valabil doar la semnalele
continui. Un semnal eşantionat (întrerupt periodic), la
care valoarea funcţiei f(t) se cunoaşte numai la momente discrete, va
avea limitată superior pulsaţia maximă din spectru, cu toate că semnalul
continuu din care provine poate avea componente spectrale cu pulsaţii oricât de
mari. Este vorba de teorema eşantionării sau teorema lui Shannon (formulată în 1948),
cunoscută şi ca teorema Nyquist–Shannon, care
arată, în esenţă, că un semnal eşantionat nu poate conţine armonice cu pulsaţia
mai mare de p /d t (frecvanţa maximă fiind n/2, n=numărul
de eşantioane pe secundă). Demonstraţia este destul de pretenţioasă dar
se poate înţelege şi empiric. Admiţând că dorim să cunoaştem amplitudinea şi
faza iniţială ale unei componente armonice cu pulsaţia oarecare w, pentru a putea fi determinate trebuie rezolvat un sistem de două
ecuaţii ale armonicei, în care vor apare valorile cunoscute din semnal la orice
momente de forma t şi t + d t. Dacă respectiva componentă armonică are perioada mai
mică decât intervalul d t este evident că ecuaţiile nu mai pot exista, de aceea
armonica cu pulsaţia cea mai mare nu poate avea o perioadă mai mică decât de 2
ori valoarea d t. Problema
se poate pune şi invers, dacă dorim ca o transmitere pe eşantioane a semnalului
să aibe componente cu pulsaţii până la o valoare wmax atunci eşantionarea trebuie făcută cu o valoare d t mai mică decât p / wmax.
Astăzi această teoremă are o importanţă covârşitoare în transmisiile digitale
audio-video dar şi de internet cu implicaţii în fidelitate, rezoluţie,
densitate de informaţie, lărgime de bandă etc. De exemplu, un semnal video
eşantionat cu 5000 kbps (formatul MPEG 2 la calitatea maximă) asigură
procesarea informaţiilor din semnal până la o frecvenţă de 2,5 MHz. Dar spectrul continuu, chiar şi pentru semnale eşantionate, mai oferă şi
alte perspective.
De exemplu identificarea originii unui semnal
pe bază de amprentă spectrală (în cazul vocilor, pe bază de amprentă vocală,
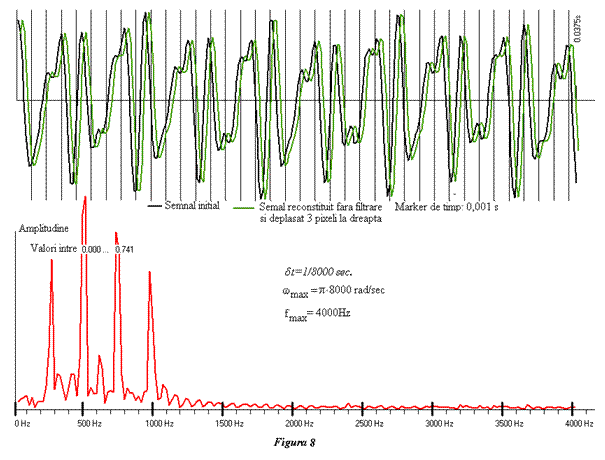
proprie oricărei persoane, precum amprenta dactiloscopică), figura 8, unde se
vede spectrul vocalei „a” rostită de autor şi discretizată cu 8000 de eşantioane
pe secundă, ceea duce la o frecvenţă maximă de 4000 Hz a componentelor din
spectru. Captarea şi digitizarea semnalului am făcut-o cu un microfon cuplat la
calculator şi folosind utilitarul Sound Recorder, rezident pe Windows, care
permite setarea eşantionării după dorinţă. Apoi am prelucrat fişierul wav
astfel creat cu un soft propriu, construit pe baza transformatei Fourier
clasică şi a rezultat un spectru tot în formă discretă, nici nu ar fi fost
posibil altfel pe cale numerică. Multe aparate şi aplicaţii soft care oferă pe
un display spectre sub formă de bare variabile pe înălţime folosesc şi aici
TFR, din motive de calcul simplificat şi rapid, oferind rezultate spectaculoase
dar insuficient de corecte pentru o cercetare detaliată a spectrului. Se mai pot face filtrări destul de interesante. Aşa cum există o
transformată Fourier de la semnal la spectru, există şi o transformată Fourier
inversă (care, din fericire, nu mai are varianta „rapidă”), de la spectru se
reface semnalul, tot cu o integrală improprie din funcţii complexe. Numai că,
în procesul de refacere a unui semnal din spectrul său, se poate modifica după
dorinţă amplitudinea componentelor spectrale ale anumitor frecvenţe şi astfel se
poate schimba timbrul vocii, se pot accentua componenele care interesează sau se
pot reduce ori elimina componentele nedorite (zgomotul). Pentru aceste operaţii
nu se mai poate folosi TFR ci numai transformata clasică şi, mai mult, mai este
nevoie de o nouă teoremă care mult timp a „plutit” în aer sub o formă empirică.
Personal am realizat o demonstraţie analitică
exactă a acesteia, care a fost omologată la o conferinţă internaţională de procesare
a semnalelor cu mulţi ani în urmă [4], ca o a doua teoremă a eşantionării sau ca o
complementară a teoremei lui Shannon. In esenţă, pentru ca transformarea
inversă de la spectru la semnal să fie corectă, se impune ca numărul de
eşantioane din spectru să fie cel puţin jumătate plus 1 din numărul de
eşantioane din semnalul căruia i s-a aflat spectrul. În caz contrar (de
exemplu, chiar dacă lipsesc numai 2---3 eşantioane spectrale din cîteva sute) semnalul
refăcut nu mai are nimic comun cu cel iniţial. În figura 8 semnalul iniţial
este desenat cu negru iar semnalul reconstituit fără filtrare, deci pe baza
întregului spectru, este desenat cu verde şi deplasat 3 pixeli la dreapta
pentru a se distinge mai uşor de semnalul iniţial. Se vede o bună asemănare a
celor două semnale.
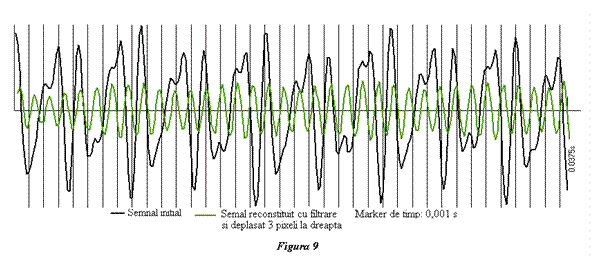
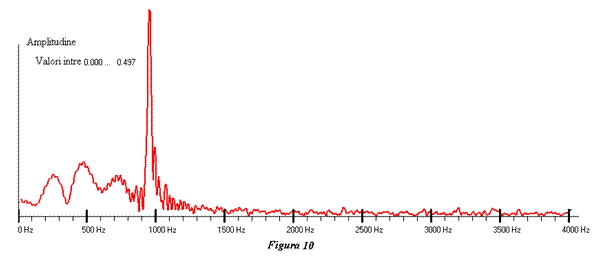
Semnalul desenat cu verde în figura 9 este prelucrarea
semnalului desenat cu negru şi filtrat „trece sus” pentru frecvenţe peste 800
Hz , spectrul său se vede în figura 10. Regenerarea exactă a semnalelor prin filtrare este foarte anevoioasă, de
exemplu pentru un semnal cu durata de 10 secunde din domeniul audio, prelevat
cu 32000 de eşantioane pe secundă, care a fost refăcut prin modificarea
spectrului, calculatorul a lucrat cca 12 minute în care a prelucrat fiecare
eşantion din cele 320000 folosind pentru fiecare prelucrare cele 160001
eşantioane din spectru. 4.
Pentru amatori. Prelucrarea semnalelor conform
celor arătate mai sus a fost făcută cu softuri proprii. Le consider utile la
dimensionarea multiplicatoarelor de frecvenţă dar şi la evaluarea spectrului
(prin serie sau transformată Fourier) unui anumit tip de semnal. Le pun la
dispoziţie oricărui doritor, dacă îmi scrie pe adresa mea de e-mail. Softurile care
folosesc transformata Fourier pentru analiza spectrală au
dialogurile cu utilizatorul în limba engleză, deoarece l-am folosit – şi mai
este folosit de colegi – pentru lucrări prezentate în străinătate. În desenele
din această lucrare am tradus toate textele în limba română. Bibliografie. [1] Gh. Oproescu, Gh. Cauteş. Metode numerice şi aplicaţii. Editura TEHNICA-INFO,
Chişinău 2005, ISBN 9975-63-254-8 [2] Gheorghe Oproescu, Carmen
Debeleac. About of the non-harmonical periodical signal spectrum.
Romanian Journal of Acoustics and Vibration, dec. 2007, ISSN 1584-7284, pg.
79-82. (apărut 2008) [3] Gheorghe Oproescu. Spectral
Function of the Wave and Quantum Physic. Romanian Journal of Acoustics and
Vibration, iune 2007, ISSN 1584-7284, pg. 31-34. (apărut 2008) [4] Gheorghe Oproescu. Spectral
analysis and regeneration of the numerical signals. Proceedings of the 8th
International Conference on Signal Processing (SIP’09), Istanbul, Turkey, May
30 – June 01 2009, ISSN 1790-5117, pg. 55-60 (clasificare ISI).
Articol aparut la 28-2-2015 7785 Inapoi la inceputul articolului | |||||||||||||||||||||||||||||||||||||||||||||||
|
Comentariul trebuie sa se refere la continutul articolului. Mesajele anonime, cele scrise sub falsa identitate, precum si cele care contin (fara a se limita la) atac la persoana, injurii, jigniri, expresii obscene vor fi sterse iar dupa caz se va ridica dreptul de a posta comentarii.
| |||||
Opiniile exprimate în articole pe acest site aparţin autorilor şi nu reflectă neapărat punctul de vedere al redacţiei.
|
Copyright © Radioamator.ro. Toate drepturile rezervate. All rights reserved
Articole | Concursuri | Mica Publicitate | Forum YO | Pagini YO | Call Book | Diverse | Regulamentul portalului | Contact |
 a cărei pulsaţie este aleasă dinainte să fie un multiplu
întreg al pulsaţiei fundamnetale, respectiv 1
a cărei pulsaţie este aleasă dinainte să fie un multiplu
întreg al pulsaţiei fundamnetale, respectiv 1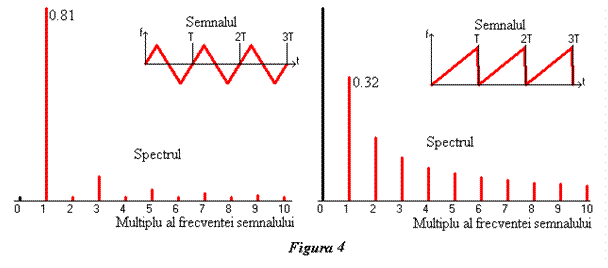
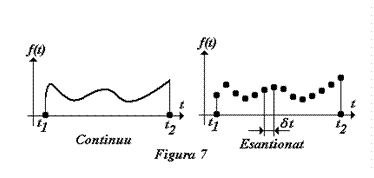 Un
semnal eşantionat este un semnal periodic sau neperiodic întrerupt periodic în
timp. Asta înseamnă că semnalul nu mai este continuu iar valorile sale sunt
cunoscute numeric (digital) numai la momente discrete, separate de intervale
regulate de timp
Un
semnal eşantionat este un semnal periodic sau neperiodic întrerupt periodic în
timp. Asta înseamnă că semnalul nu mai este continuu iar valorile sale sunt
cunoscute numeric (digital) numai la momente discrete, separate de intervale
regulate de timp