O SPERANŢĂ: ANTENE CU GABARIT REDUS PENTRU UNDE SCURTE
Aceasta a fost o pacaleala de 1 aprilie
Gheorghe Oproescu - Tavi YO4BKM
În
aglomeraţiile urbane din zilele noastre, dar şi în condiţii mai speciale, cum
ar fi cele în portabil de plăcere (o ieşire în natură, prilej de a comunica şi
altora evenimentul) antenele pentru traficul pe frecvenţele inferioare sunt o
problemă. Improvizaţii, inovaţii, construcţii de firmă, adaptoare, păreri pro
şi contra, există o vastă literatură în domeniu, puternic întreţinută de un
foarte diversificat folclor mai mult sau mai puţin justificat. În concret,
despre ce poate fi vorba? Despre un conductor electric cu anumite forme şi
dimensiuni astfel încât să se poată acorda pe frecvenţa de lucru cu pierderi
cât mai reduse, să transforme cât mai multă energie de radiofrecvenţă în
energie a undelor electromagnetice şi să aibe o caracteristică de radiaţie cât
mai favorabilă pentru traficul dorit. Ei bine, aceste trei „cât mai” împing
soluţiile tehnice în direcţii atât de diferite încât singura şansă este de a
face compromisuri. Compromisuri nedeterministe deoarece de la antenă la antenă
diferă vecinătăţile, înălţimea faţă de sol sau altele.
O
soluţie modernă, puţin cunoscută dar deja aplicată, o oferă construcţiile bazate
pe o recentă teorie din matematică, teoria fractalilor.
1.
Ce sunt fractalii.
Fractalii au apărut foarte recent. Se spune că teoria lor s-a născut
brusc, fără pregătiri preliminare, în 1975 odată cu lucrarea matematicianului
Benoit Mandelbrot intitulată "O teorie a seriilor fractale". Primul
interes s-a manifestat în lumea naturală, prin cartea considerată un adevărat
manifest, "Geometria fractală a naturii" a aceluiaşi Mandelbrot, în
1982. În esenţă, Mandelbrot nu a fost întru totul un original. Ce a făcut el a
fost să reunească într-un aparat matematic unitar ceea ce mulţi înaintaşi ai săi
au produs de-a lungul secolelor. Deoarece grafica pe calculator era deja foarte
avansată în anii ’80 ai secolului trecut, modelele lui
Mandelbrot s-au extins cu mare repeziciune. Un fulg de zăpadă, buchetele verzei
de Bruxelles, cristalele, norii, lanţurile muntoase, frunzele şi altele sunt
modele naturale de fractali, azi reproduse şi geometric pe baza unor algoritmi
simpli, de la cei bidimensionali la cei tridimensionali. La un fractal nu este
complicat algoritmul de generare al său ci imaginarea unui model elementar care
să poată fi multiplicat oricât de mult, numit iniţiator. Regula sau
algoritmul după care iniţiatorul formează o nouă construcţie se numeşte generator
iar procesul de repetare a generatorului se numeşte iteraţie. Lăsând să
lucreze fantezia în aceste trei direcţii, iniţiator, generator şi iteraţie se
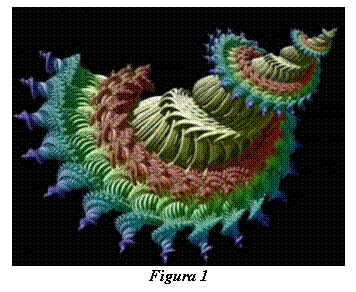
poate obţine o diversitate de construcţii. În figura 1 se prezintă un fractal
obţinut artificial, combinând forme şi culori în 3D [1].
Un
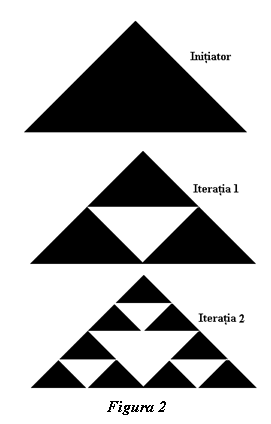
fractal simplu, în spaţiul 2D, numit „Triunghiul lui Sierpinski”, se vede în
figura 2, de unde se poate înţelege şi modul de generare al său. Iniţiatorul constă
dintr-un triunghi oarecare, trasat pe o coală de hârtie. Se fixează mijloacele
fiecărei laturi care vor servi ca vârfuri pentru a forma alt triunghi, a cărui
suprafaţă nu se mai ia în considearre. Suprafeţele rămase formează alte
triunghiuri care seamănă cu iniţiatorul. Pe laturile fiecărui triunghi nou
format se fixează mijloacele, care servesc drept vârfuri pentru alte
triunghiuri care nu se mai iau în considerare. Pe suprafeţele rămase se
formează alte triunghiuri asemănătoare cu iniţiatorul. Pe laturile fiecăruia se
fixează mijloacele ... etc. În acest exemplu iniţiatorul este primul triunghi, generatorul
constă în a construi triunghiri formate cu vârfurile pe jumătăţile fiecărei
laturi ale triunghiurilor nedecupate iar iteraţia este repetarea generatorului
de la iniţiator la triunghiuri din ce în ce mai mici.
Pentru
cine doreşte să folosească drept iniţiator un pătrat regula este aceeaşi, cu
câteva observaţii:
-fiecare
latură a iniţiatorului se înparte în trei părţi egale, prin punctele rezultate
se duc paralele la laturile iniţiatorului, după care pătratul din centru nu se
mai ia în considerare;
-rămân
în jurul lui 8 pătrate din care fiecare devine iniţiator la care se aplică
acelaşi procedeu;
-continuând
iteraţiile se obţine covorul lui Sierpinski.
Pentru
alte poligoane se pot deduce reguli de generare asemănătoare.
Fractalii
au început să ocupe tărâmul artelor şi să treacă de la modele bidimensionale la
altele tridimensionale. Perfecţionându-se şi modelele matematice s-a aflat că
fractalii se includ în aşanumita teorie a complexităţii de care aparţin teorea
haosului, teoria catastrofelor, teoria structurilor disipative [1]. Acesata din urmă teorie a permis să se facă trecerea de la fractalii
teoretici la elemente practice care să-i foloseacă, precum antenele care, în
esenţă, sunt structuri disipative.
2.
Antene realizate din factali.
Pentru
a se restrânge spaţiul ocupat de conductorul unei antene filare acesta poate fi
pliat, teoretic, după orice formă geometrică apoi modelat cu softuri specifice.
Dar folosind forme rezultate din teoria fracatalilor se obţin construcţii
deosebit de avantajoase în privinţa adaptării, randamentului şi
caracteristicilor de radiaţie. De ce? Se va vedea din prezentarea detaliată a
două categorii de fractali utilizabili şi din cercetarea particularităţilor
lor.
2.1. Fractali obţinuţi din iniţiator rectiliniu.
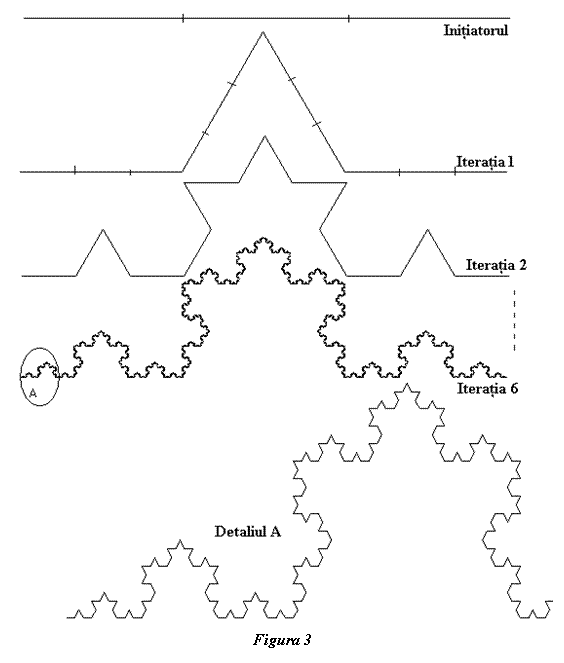
După
cum se vede din figura 3, iniţiatorul este un conductor rectiliniu, de o
anumită lungime l, care se împarte în trei părţi egale. La prima
iteraţie segmentul de la mijloc se elimină şi este înlocuit cu două segmente de
aceeaşi lungime care nu se pot aşeza decât formând un unghi. Aşa s-a obţinut
forma din iteraţia 1. Fiecare segnent din iteraţia 1 se împarte în câte trei
părţi egale, segmentul din mijloc se elimină şi se înlocuieşte cu două segmente
de aceeaşi lungime, cu vârful spre exterior. Se obţine forma din iteraţia 2. Dacă
„n” este numărul de ordine al iteraţiei, lungimea însumată a tuturor
segmentelor este 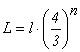 , adică cu
mult mai mare decât lungimea iniţiatorului, l. Am creat un soft care să
genereze şi grafic acest fractal cu oricâte iteraţii se doreşte. De exemplu, la
a şasea iteraţie fractalul are o lungime desfăşurată de 5,62 ori mai mare decât
lungimea iniţiatorului. Aşadar, în acelaşi gabarit (distanţa dintre
extremităţile iniţiatorului) se poate construi un contur din segmente a căror
lungime totală este de 5,62 ori mai mare. Sau invers, o anumită lungime poate
fi redusă, după 6 iteraţii, la un gabarit de 5,62 ori mai scurt. , adică cu
mult mai mare decât lungimea iniţiatorului, l. Am creat un soft care să
genereze şi grafic acest fractal cu oricâte iteraţii se doreşte. De exemplu, la
a şasea iteraţie fractalul are o lungime desfăşurată de 5,62 ori mai mare decât
lungimea iniţiatorului. Aşadar, în acelaşi gabarit (distanţa dintre
extremităţile iniţiatorului) se poate construi un contur din segmente a căror
lungime totală este de 5,62 ori mai mare. Sau invers, o anumită lungime poate
fi redusă, după 6 iteraţii, la un gabarit de 5,62 ori mai scurt.
 Mărind numărul de iteraţii segmentele vor forma la limită, adică pentru Mărind numărul de iteraţii segmentele vor forma la limită, adică pentru
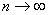 , o linie
curbă cu lungimea infinită între două extremităţi finite, marcate de capetele
iniţiatorului. De precizat că linia nu este continuă şi, matematic, nu este
derivabilă. Iată cum o lungime de conductor pliat după un fractal de acest gen
poate ocupa un gabarit mult mai redus între extremităţile fractalului, decât
între extremităţile conductorului rectiliniu. Prezint mai jos un şir de valori
care arată de câte ori se reduce gabaritul fractalului funcţie de numărul de
iteraţii. , o linie
curbă cu lungimea infinită între două extremităţi finite, marcate de capetele
iniţiatorului. De precizat că linia nu este continuă şi, matematic, nu este
derivabilă. Iată cum o lungime de conductor pliat după un fractal de acest gen
poate ocupa un gabarit mult mai redus între extremităţile fractalului, decât
între extremităţile conductorului rectiliniu. Prezint mai jos un şir de valori
care arată de câte ori se reduce gabaritul fractalului funcţie de numărul de
iteraţii.
|
Numărul de iteraţii
|
7
|
8
|
9
|
10
|
15
|
|
De câte ori se
reduce gabaritul între extremităţile fractalului
|
7,49
|
9,98
|
13,32
|
17,75
|
74,83
|
Am
mai arătat că se poate imagina o mulţime de moduri de a plia un fir astfel
încât să ocupe un gabarit mult mai mic. Numai că la fractalul descris se
evidenţiază nişte avantaje. Cercetând oricare din segmentele care compun
fractalul din figura 3 se observă că nu există decât trei categorii:
-
segmente orizontale;
-
segmente înclinate spre stânga cu 30 de grade faţă
de verticală;
-
segmente înclinate spre dreapta cu 30 de grade faţă
de verticală;
Se
mai remarcă un amănunt: după prima iteraţie fractalul nu se mai extinde nici pe
verticală, deşi lungimea însumată a segmentelor creşte până la infinit.
În
felul acesta o lungime de conductor de 42 m (semiunda la banda de 80 m) se
poate reduce la un gabarit de ordinul metrilor sau zecilor de centimetri
folosind un fractal cu cel puţin 10 iteraţii.
La
telefoanele mobile moderne antenele se realizează după acest procedeu,
asigurându-se o lungime corectă a conductorului într-un gabarit de ordinul a
câţiva cm. Datorită dimensiunilor reduse realizarea se face în tehnica
circuitelor imprimate sau tehnici strip ori microstrip. Randamentul acestor
antene este foarte ridicat şi, în plus, datorită dispunerii segmentelor în
plane paralele într-un spaţiu foarte redus, radiaţia antenei creşte în
eficienţă.
2.2.
Fractali obţinuţi din iniţiator triunghiular
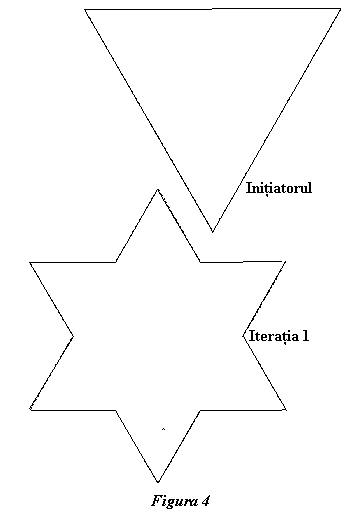
O eficienţă mărită se obţine cu un fractal construit pe baza unui
iniţiator triunghiular, figura 4. Fiecare latură a triunghiului generează
fractali ca în cazul precedent, adică se împarte în trei segmente egale iar
segmentul din mijloc este înlocuit cu alte două segmente egale, formând un
unghi cu vârful în exterior. În felul acesta la prima iteraţie perimetrul
iniţatorului a crescut de 1,33 ori.
Continuând
iteraţiile pentru generarea fractalilor, cu ajutorul altui soft propriu, am
putut genera forme oricât de avansate. Aceşti fractali seamănă cu un fulg de
zăpadă şi se numesc curbele lui Koch. În figura 5 se arată un fractal la iteraţia
5. Şi de data acesata se remarcă aceeaşi caracteristică, segmentele ocupă doar
trei direcţii, indiferent cât de mult creşte ordinul iteraţiilor.
Avantajul
fractalilor cu iniţiator triunghiular (sau orice poligon, adică un contul închis)
constă în realizarea de antene de genul bucle închise, cu avantajele deja
cunoscute:
-
mai puţin zgomotoase;
-
o impedanţa de radiaţie ridicată, mai apropiată de
impedanţa mediului în care radiază, deci o cuplare mai bună cu mediul.
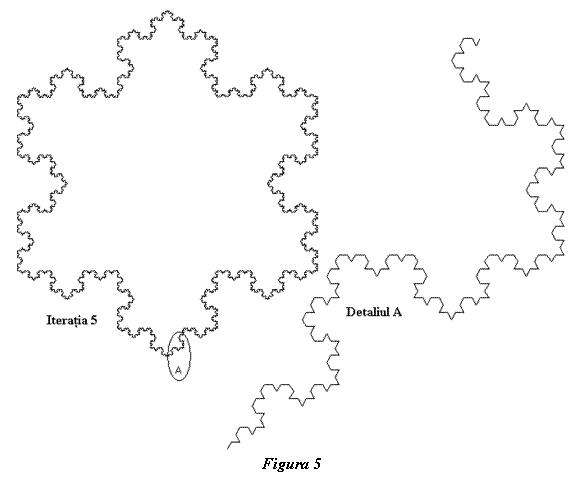
Şi la acest fractal lungimea însumată a segmentelor devine infinit de
mare după un număr infinit de mare de iteraţii, fără să se mărească gabaritul
ocupat de antenă. Creşterea lungimii unui fractal la iteraţia „n” în comparaţie
cu perimetrul iniţiatorului, pe care îl notez tot cu l, se face după
aceeaşi formulă ca la
fractalul precedent. În caz concret, un fractal cu 12 iteraţii reduce gabaritul
unui dipol rectiliniu de 31 de ori, astfel că o buclă cu un perimetru de 42 m
va ocupa un gabarit redus la numai 1,3 m.
3.
Concluzii.
Antenele
construite după geometria fractalilor se folosesc deja. Din punct de vedere
constructiv nu există nicio deosebire dictată de lungimea de undă. Răspândirea
lor redusă în domeniul undelor decametrice şi metrice este determinată, în
primul rând, de considerente comerciale. Telefoanele mobile se fabrică şi se
vând împreună cu antenele lor în număr incomparabil mai mare decât antenele
pentru unde decametrice sau metrice pentru care o investiţie nouă ar fi greu de
amortizat. Datorită gabaritului redus al antenelor telefoanelor mobile realizarea
lor prin imprimare sau tehnici strip ori microstrip automatizate duce la o
productivitate ridicată, practic fără manoperă directă. Mai mult, antenele
fractal fac obiectul unor brevete de invenţii recente care pun şi ele probleme
de costuri la achiziţionarea unui brevet în scopuri comerciale. Dar nu opreşte
nimeni ca în particular să se experimenteze antene fractal, cu condiţia să nu fie
comercializate, pentru a nu fi încălcate drepturile celor care deţin brevetele.
Aşa
cum am arătat mai sus, un conductor cu lungimea de 42 m poate ocupa, sub formă
de fractal, un spaţiu plan cu laturile de maxim 1,5 m. Dacă cineva doreşte să
„migălească” mai mult la antenă, o poate reduce chiar şi mai mult, fără a
afecta caracteristicile de lucru ale antenei.
Numai că aplicarea la unde scurte deşi este descrisă corect
mai sus, nu este posibilă din următoarele motive:
-
Un fractal ca cel din figura 3
are, numai după 6 iteraţii, un număr de 4096 de segmente. Numărul de segmente,
îl notez cu N, se calculează cu 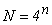 , n fiind
numărul de iteraţii. Pentru un conductor cu lungimea desfăşurată de 42 m,
fiecare segment are o lungime de cca 10 mm. Cele 6 iteraţii reduc gabaritul
antenei (distanţa dintre extremităţile fractalului) de 5,62 ori, astfel încât
acesta devine 7,47 m. , n fiind
numărul de iteraţii. Pentru un conductor cu lungimea desfăşurată de 42 m,
fiecare segment are o lungime de cca 10 mm. Cele 6 iteraţii reduc gabaritul
antenei (distanţa dintre extremităţile fractalului) de 5,62 ori, astfel încât
acesta devine 7,47 m.
-
Rezultă un gabarit destul de mare
care nu permite realizarea unei antene „autoportante”, cele 4096 de segmente
trebuie să fie fixate pe o suprafaţă rigidă pentru a nu schimba forma
fractalului la suspendarea antenei. O reducere mai drastică a gabaritului, de
exemplu cu un fractal obţinut după 10 iteraţii care duce la un gabarit de 2,36
m, va conduce la peste un milion de segmente a căror lungime devine de numai
0,04 mm. Cât va trebui să fie diametrul unui astfel de conductor? Cât va dura
„migala” asamblării milionului de segmente?
-
La telefoanele mobile se rezolvă
problema reducerii gabaritului unor antene cu lungimea desfăşurată de ordinul
centimetrilor, astfel încât un fractal obţinut cu puţine iterări poate ocupa o
suprafaţă foarte mică şi se poate realiza pe un suport rigid. Puterea redusă a
acestor telefoane nu obligă la conductori cu secţiune mare, astfel încât
fractalul real nu are abateri mari faţă de cel teoretic care nu ţine cont de
grosimea liniei cu care a fost construit.
În final, problema realizării unui fractal pentru
antene care lucrează în unde scurte seamănă cu alte situaţii imposibile, deşi
par rezolvabile la prima vedere. Una este cunoscuta legendă a premiului pretins
ca răsplată de inventatorul jocului de şah. El a cerut un bob de grâu pentru
primul pătrat de pe tabla de şah, două boabe pentru al doilea, patru boabe
pentru al treilea, opt boabe pentru al patrulea ş.a.m.d. în progresie
geometrică. Calculând numărul de boabe, egal cu 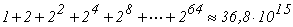 , acesta nu
putea fi asigurat de producţia pe câteva secole. O altă situaţie este mai concretă.
Dacă se îndoaie o coală de hârtie de 50 de ori (nu în 50 de straturi, ci cu 50
de îndoituri), în speranţa că cineva va reuşi să le facă pe toate, se va obţine
un pachet cu , acesta nu
putea fi asigurat de producţia pe câteva secole. O altă situaţie este mai concretă.
Dacă se îndoaie o coală de hârtie de 50 de ori (nu în 50 de straturi, ci cu 50
de îndoituri), în speranţa că cineva va reuşi să le facă pe toate, se va obţine
un pachet cu 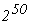 foi, gros de
la Pământ până la Soare. foi, gros de
la Pământ până la Soare.
Bibliografie
[1]
http://mariacalinescu.eu/e-business/ce-sunt-fractalii/
- Gheorghe Oproescu - Tavi YO4BKM
-
Articol aparut la
31-3-2015
10273
Inapoi la inceputul articolului
|




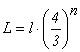 , adică cu
mult mai mare decât lungimea iniţiatorului, l. Am creat un soft care să
genereze şi grafic acest fractal cu oricâte iteraţii se doreşte. De exemplu, la
a şasea iteraţie fractalul are o lungime desfăşurată de 5,62 ori mai mare decât
lungimea iniţiatorului. Aşadar, în acelaşi gabarit (distanţa dintre
extremităţile iniţiatorului) se poate construi un contur din segmente a căror
lungime totală este de 5,62 ori mai mare. Sau invers, o anumită lungime poate
fi redusă, după 6 iteraţii, la un gabarit de 5,62 ori mai scurt.
, adică cu
mult mai mare decât lungimea iniţiatorului, l. Am creat un soft care să
genereze şi grafic acest fractal cu oricâte iteraţii se doreşte. De exemplu, la
a şasea iteraţie fractalul are o lungime desfăşurată de 5,62 ori mai mare decât
lungimea iniţiatorului. Aşadar, în acelaşi gabarit (distanţa dintre
extremităţile iniţiatorului) se poate construi un contur din segmente a căror
lungime totală este de 5,62 ori mai mare. Sau invers, o anumită lungime poate
fi redusă, după 6 iteraţii, la un gabarit de 5,62 ori mai scurt. 
