Gheorghe Oproescu - Tavi YO4BKM

1. Coordonate, locații și locatoare.

Odată cu Renașterea, în Europa se dezvoltă școli proprii care au dezvoltat sistemul de coordonate geografice așa cum este cunoscut astăzi. Pe o suprafață sferică este mult mai simplu să evaluezi poziția și distanța ca măsuri ale unor unghiuri deoarece sunt mai ușor de măsurat și oferă date cu caracter practic imediat. Dacă o distanță pe sferă este cunoscută sub formă de valoare a unui unghi la centrul sferei, ea este mereu aceeași indiferent cât de precis se cunoaște raza sferei. De aici provine și mila nautică, folosită și azi în navigația maritimă sau aeriană, egală cu arcul de 1’ măsurat pe un cerc cu centrul în centrul Pămîntului. Știind din măsurători cu ce viteză se deplasează o navă (noduri sau mile/oră) se află ușor în cât timp poate parcurge o distanță pe un arc de cerc de unghi cunoscut. Marea Britanie a folosit acest sistem de pe când imperiul său se întindea pe tot globul (se spunea că în Imperiul Britanic Soarele nu apunea niciodată) și a folosit hărți de navigație pe care din 1884 s-a stabilit ca meridianul care traversează renumitul Observator Regal Greenwich din Londra să fie „Meridianul Zero” de la care să se măsoare unghiurile dintre planurile corespunzătoare celorlalte meridiane. Meridianul Zero real este acum cu 102,5 metri mai departe de locul unde a fost stabilit pentru prima dată.

Din cu totul alte considerente localizarea pe suprafața terestră se mai poate face folosind o succesiune de careuri delimitate convențional de meridiane și paralele prin sistemul Maidenhead Locator System (QTH Locator sau IARU Locator), un geocod care descrie locațiile oriunde în lume, poate fi cercetat la [2]. Acum se folosește cu preponderență în formatele de log ADIF sub denumirea de GridSquare sub forma de grupuri de 4 caractere, 6 caractere sau 8 caractere și este alcătuit după cum urmează.

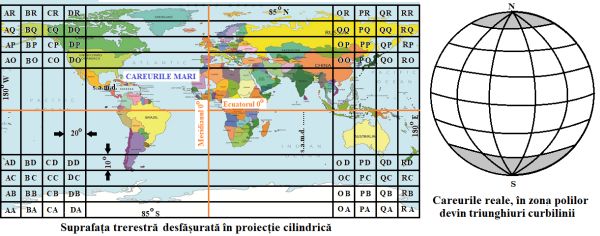
1. Sfera terestră este împărțită în 18 fâșii (felii) delimitate de meridiane și 18 fâșii delimitate de palalele. Fâșiile delimitate de meridiane încep de la meridianul 180^o W și continuă până la meridianul 160^o E, fiind notate cu literele A, B, C … P, Q, R, între ele fiind un unghi la centrul Pământului de 20^o. Ultima fâșie, notată cu R, începe de la meridianul 160^o E pentru ca, cu cele 20^o care îi revin, să devină adiacentă fâșiei A. Fâșiile delimitate de paralele încep de la Polul Sud și continuă până la Polul Nord, fiind notate cu literele A, B, C … P, Q, R, între ele fiind un unghi la centrul Pământului de 10^o. Fâșia A începe chiar din Polul Sud (90^o S), fâșia R începe la latitudinea de 80^o N pentru ca, cu cele 10^o care îi revin, să ajungă până la Polul Nord. Ordinea în care se notează în locator este prima literă pentru fâșiile delimitate de meridiane (fâșiile verticale), a doua literă pentru fâșiile delimitate de paralele (fâșiile orizontale). Fâșiile din zona ecuatorului delimitează niște patrulatere cu laturile curbe, cum sunt toate fâșiile care au a doua literă I sau J.

Careurile care încep sau se termină în unul din poli au forma unor triunghiuri curbilinii, cum sunt toate careurile care au a doua literă A sau R. Celelalte careuri au forma unor trapeze cu laturile curbe. Acestea formează careurile primare, figura 1.

Figura 1

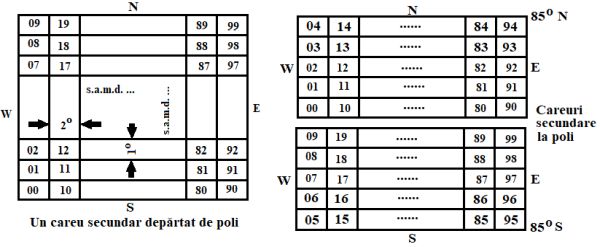
2. Fiecare careu de mai sus care are patru laturi este impărțit în 100 de careuri secundare formate din 10 fâșii verticale numerotate de la 0 la 9 dinspre vest spre est, între ele fiind un unghi la centrul Pământului de 2^o și 10 fâșii orizontale numerotate de la 0 la 9 dinspre sud dpre nord, între ele fiind un unghi de 1^o, figura 2.

Figura 2

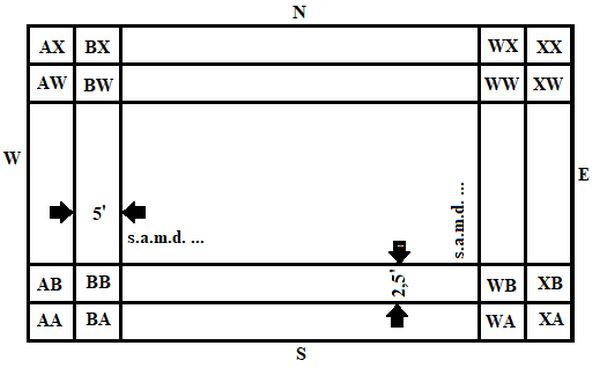
Ordinea în care se notează în locator este cu prima cifră pentru fâșiile verticale, a doua cifră pentru fâșiile orizontale. Careurile primare din apropierea polilor (de formă triunghiulară) se împart în 10 fâșii pe verticală, numerotate de la 0 la 9 dinspre vest spre est, dar careurile primare vecine cu Polul Sud (AA, BA, CA … PA, QA, RA) se împart în 5 fâșii pe orizontală numerotate de la 5 la 9 începând cu paralela de 85^o S, cele vecine cu Polul Nord (AR, BR, CR … PR, QR, RR) se împart tot în 5 fâșii pe orizontală dar numerotate de la 0 la 4, terminându-se la paralela de 84^o astfel încât, cu 1^o care revine fiecărei fâșii, să ajungă la paralela de 85^o N. În acest mod pe suprafața terestră va putea fi descrisă orice locație între paralele 85^o N și 85^o S Fiecare careu secundar se împarte în 24 x 24 de careuri formate din 24 de fâșii verticale notate de la vest la est cu literele A, B, C … W, X și 24 de fâșii orizonlate notate de la sud la nord cu literele A, B, C … W, X, formând careurile terțiare, figura 3.

Figura 3

3. Pentru mărirea preciziei de localizare, careurile terțiare se împart in 100 de careuri după schema folosită la împrțirea careurilor primare, careurile astfel formate se mai pot împărți in alte 24 x 24 de careuri după schema folosită la careurile terțiare.

Aria de cuprindere în zona Ecuatorului este de 2.222,4 x 1.111,2 km pentru un careu primar (de exemplu JJ), de 222,24 x 111,12 km pentru un careu secundar (de exemplu JJ00), de 9,26 x 4,63 km pentru un careu terțiar (de exemplu JJ00AA), de 0,926 x 0,463 km pentru un careu descris cu 8 caractere (de exemplu JJ00AA00), de 0,038 x 0,019 km pentru un careu cu 10 caractere (de exemplu JJ00AA00AA). Radioamatorii folosesc între minim 4 și maxim 8 caractere. La alte latitudini ariile acoperite de diferitele careuri sunt mai mici pe longitudine deoarece arcele de cerc paralel care formează laturile poligoanelor curbilinii nu au centrul în centrul Pământului ci în centrul cercului paralel a cărui rază scade cu creșterea latitudinii.

Sistemul Maidenhead Locator System este de preferat deoarece, folosind doar 8 caractere, localizarea are în zona Ecuatorului o eroare de maxim 30” pentru longitudine (1/2 milă nautică sau 926 m) si 15” pentru latitudine (1/4 milă nautică sau 463 m) pentru care, folosind sistemul coordonatelor geogafice, ar fi fost necesare 21 de caractere, de aproape 3 ori mai mult, transmitere mai lunga și mai susceptibila de a fi afectată de erori de preluare.

Un sistem mai vechi de localizare era compus din 5 caractere (litere și cifre) astfel [1]:
- Primele două litere delimitau un careu de formă trapezoidală (trepez curbiliniu deoarece era pe o suprafașă sferică), fiecare trapez avea o deschidere de 2^o pe direcția W-E și de 1o pe direcția N-S. Prima literă indica „fâșia verticală” de 2^o, se foloseau literele A, B, C … Y, Z spre Est, în sens invers Z, Y, X … B, A spre vest, începând cu Meridianul Zero. A doua literă indica „fâșia orizontală” lată de 1o spre nord, începând cu paralela de 40^o N, se foloseau literele A, B, C … Y, Z, sub paralela de 40^o N se foloseau literele Z, Y, … B, A.
- Fiecare trapez primar era împărțit în 80 de trapeze secundare, pe fâșii numerotate cu 0, 1, 2, 3 … începând cu latura de nord până la 7 lângă laura din sud ca primă cifră și pe fâșii verticale numerotate cu 1, 2 … 8, 9, 0 ca a doua cifră.
- Fiecare trapez secundar se impărțea în 9 trapeze terțiare notate h, a, b pe linia de nord, g, j, c pe linia de mijloc și f, e, d pe linia de sud. În preajma Ecuatorului aceste trapeze au dimensiunile de 7,408 x 4,630 km.

Prin anii ’70 eram YO7BKM, locuiam in Pitești (cartier Trivale) și aveam locatorul ME15h. Cercetând prin logurile vechi, am găsit că l-am folosit până în august 1984, după care a fost înlocuit cu locatorul Maidenhead, prea limitat la spațiul european.

2. Distanțe și azimuturi.

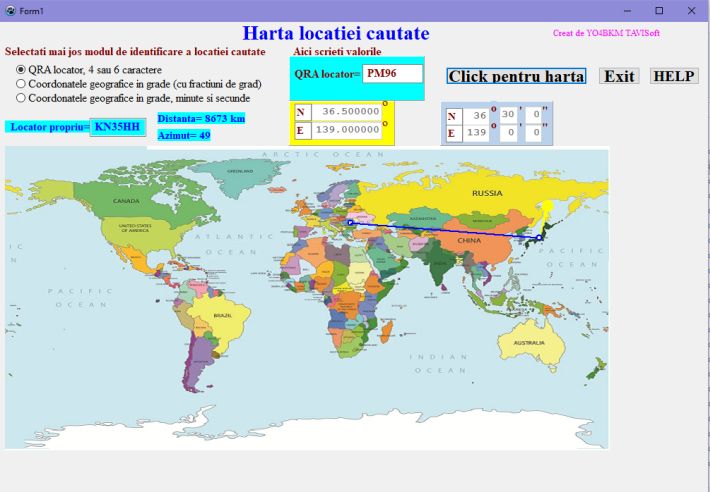
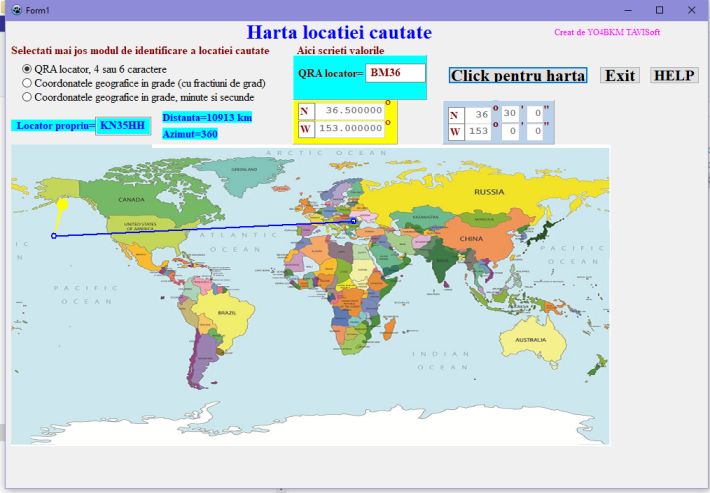
În figura 4 este o captură ecran după o aplicație proprie unde am fixat locatorul meu (KN35HH) si locatorul partenerului (PM96), stația japoneză JJ1GLK. Aplicația arată o distanță de 8673 km față de partenerul localizat pe 4 caractere și un azimut de 49^o. În acest caz am programat ca, dacă vreunul din locatoare are 4 caractere iar celălalt are 6 caractere, aplicația sa completeze locatorul mai scurt cu caracterele MM, în centrul careului secundar. Datele furnizate de JTDX folosit la modurile digitale sunt azimut 49^o , distanța de 8663 km. Diferențele sunt determinate de valoarea razei terestre din softurile de lucru, de completarea careului terțiar cu caracterele MM și din trunchierea calculelor. Ciudat este că, deși azimutul are valoarea de 49^o, pe hartă apare ca fiind mai mare de 90^o. Acest lucru se întâmplă deoarece harta este desfășurata unei proiecții cilindrice a suprafeței sferice terestre, la care marginile extreme din stânga și din dreapta (latitudinile de 180^o E și 180^o W) nu se suprapun ca pe sferă sau ca pe cilindru. În cazul sferei, arcul cercului mare al distanței (cerc cu centrul în centrul Pământului) trece cu atât mai aproape de poli cu cât partenerul este plasat mai aproape de longitudinea meridianului opus mie. De exemplu, un partener aflat pe același cerc paralel cu JJ1GLK, dar pe un meridian la 180 de grade față de meridianul meu (locatorul partenerului devine BM36), va avea un azimut de 360^o, figura 5, distanța este de 10913 km, deși pe hartă azimutul apare ca fiind puțin mai mic decât 270^o.

La distanțe mici, de câteva sute de km astfel de devieri sunt neglijabile.

Deși suntem legați de o suprafață sferoidală, deși tot Universul apropiat sau îndepărtat este departe de a fi plan sau rectiliniu, deși se cunosc astfel de lucruri cu sute, chiar cu mii de ani în urmă, în școală nu se învață despre geometria sferică, cunoscută în detaliu doar de navigatori sau de astronomi. Geometria sferică nu este mai complicată decât geometria euclidiană din moment ce a fost construită cu milenii în urmă, totul depinde de obișnuință. Dar este surprinzător să afli după mulți ani de școală că trăim de fapt într-o lume în care cele mai evidente deosebiri sunt:
- Liniile drepte sunt cercuri care au centrul în centrul sferei.
- Mărimile liniare sunt înlocuite de arce și unghiuri, inclusiv în teorema lui Pitagora aplicată pe o sferă.
- Drumul cel mai scurt dintre doua puncte nu mai este o linie dreaptă trasă pe o hartă ci este o linie curbă pe un arc de cerc cu centrul în centrul sferei (cerc mare). Acest lucru crează probleme la interpretarea hărților care, fiind desfășurări sau proiecții ale unei sfere pe un plan, denaturează unghiurile sau/și distanțele.
- Liniile paralele se pot întâlni.
- Suma unghiurilor unui triunghi este mai mare de 180^o.

Cu ocazia acestei prezentări țin să arăt o întâmplare din sec. XVIII. Atunci Academia Franceză de Științe a reușit să îi convingă pe marii producători de bunuri și pe marii comercianți să îi finanțeze o expediție costisitoare pentru măsurarea mai exactă a circumferinței terestre. Vechea măsurătoare făcută de Eratostene dădea o valoare de 252.000 de stadii egiptene, respectiv între 39.060 km și 40.320 km după cum se evaluează azi o stadie între 155---160 m. În acei ani ai sec. XVIII producția manufacturieră era treptat înlocuită de mașinism și industrializare mărind volumul mărfurilor și aria lor de circulație pe glob. În calea acestui progres se resimțea tot mai mult frâna pusă de mulțimea de unități de măsură pentru lungimi și suprafețe alături de prețurile și tarifele exprimate funcție de valoarea diferitelor măsuratori și conversii. Deoarece orgoliile naționale nu acceptau ca măsurile unei țări să devină masuri internaționale, Academia Franceză de Științe a venit cu propunerea să se măsoare foarte exact circumferința terestră care, împărțită într-un mare număr de diviziuni, să formeze un etalon de lungime „natural”, independent de naționalitate. Cu această „găselniță” au obținut fianțarea cu care au măsurat în 1790 un arc de cerc destul de lung, intre o clopotniță din Dunkerque și castelul Montjuïc din Barcelona, găsind o lungime de 1075,8 km pe un arc de meridian de 580,13’. Extrapolând la un unghi de 360^o s-a ajuns ca, în 1793, Franța să definească metrul astfel încât să încapă de 40.000.000 de ori pe o circumferință terestră. Prin anii ’50 ai secolului trecut, pe când eram elev în școala generală, învățam la fizică despre metru că este „a zecea miloana parte din sfertul de meridian terestru”. Sigur își mai amintesc și alții de aceasta definiție. Dar „fiannțatorii” expediției franceze condusă de Jean Baptiste Joseph Delambre și Pierre Méchain nu au surprins niște detalii simple: ca să măsori ceva, ai nevoie de un etalon de măsură care să se cuprină de exact 40.000.000 de ori intr-o circumferință. Că doar nu era să pună pe o planșetă meridianlul terestru și să îl împartă în 40 de milioane de părți egale. Deci etalonul metrului era deja fixat, cel puțin în linii mari, iar Franța a câștigat dublu, a impus în lume propriul etalon, dar a și făcut o măsurătoare geodezică importantă la acele timpuri. A fost, probabil, cea mai valoroasă inițiativă a Academiei Franceze de Științe deoarece mai târziu a făcut multe gafe cu teoriile sale despre meteoriți considerați a fi pietre aruncate de vulcani sau despre imposibilitatea zborului cu aparate mai grele decât aerul respingând proiectul de aeroplan al lui Traian Vuia.

Azi se știe că circumferința terestră are 40.075,017 km la Ecuator (raza terestră de 6.378,137 km ), 40.007,863 km peste poli (raza terestră de 6.367,449 km) și s-a convenit ca 1 milă nautică să corespundă la 1,852 km în sistemul metric iar raza terestră folosită în calcule să fie de 6366,7 km.

Bibliografie
[1] Ion Mihail Iosif . Traficul radioamatorului, Editura STADION, București, 1972
[2] TK5EP https://www.egloff.eu/qralocator/

Gheorghe Oproescu - Tavi YO4BKM

Articol aparut la 9-8-2024

1184