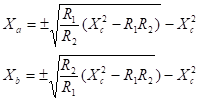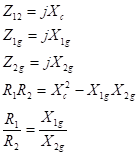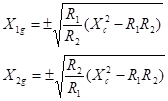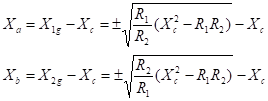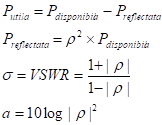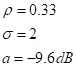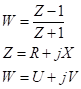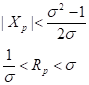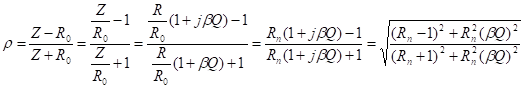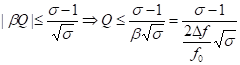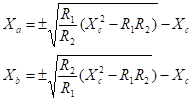ing. Mihai Stocec YO3AYX

1 Introducere

In acest articol  prezint o abordare mai amănunţită a modului de dimensionare a celui mai cunoscut etaj din cadrul instalaţiei de emisie-recepţie şi anume circuitul de adaptare cu antena, sau cum este apelat în cadrul literaturii radioamatorilor, “Transmatch”.

Analiza este axată pe gama undelor scurte extinsă, 1.8 – 30 MHz, dar conceptul poate fi folosit pentru oricare altă zonă de frecvenţe.

Abordarea se referă la modul cum trebuie dimensionată o reţea de adaptare astfel încât să se atingă mai multe deziderate privind transferul de putere. Sunt exploatate capabilităţi noi ale ale reţelelor de adaptare pe direcţia unui acord mai facil pe frecvenţa de lucru.

2 Despre circuitele de adaptare

Circuitul de adaptare este un cudripol reactiv, inserat între borna de antenă a staţiei şi antenă, sau indirect, la antenă prin fiderul de alimentare.

Adaptarea în radiofrecvenţă are două aspecte, şi anume:

·         Adaptarea pentru transfer maxim de putere. Asigură transferul maxim de putere de la generator la sarcină.

·         Adaptarea pe imagini. Asigură ca impedanţele văzute în cele două sensuri, la punctul de joncţiune dintre un generator şi sarcină, să fie egale. Este o condiţie mai generală de adaptare în care impedanţele generatorului şi a sarcini sunt mărimi complexe. Adaptarea pe imagini este egala cu cea pentru transferul maxim de putere atunci când cele două impedanţe sunt rezistive.

Problema generală a adaptării rezidă în transformarea unei impedanţe de sarcină într-o altă impedanţă optimă pentru generator.

Trebuie menţionat încă de la început că atât antena, în cazul nostru de studiu, cât şi staţia radio la borna de antenă prezintă impedanţe complexe.

Pe de altă parte, în cazul traficului de radioamatori, benzile de lucru sunt relativ înguste, astfel că se poate admite ca studiul adaptării să fie abordat pentru impedanţe constante, de natură rezistivă. Se face presupoziţia că partea reactivă a celor două impedanţe va fi absorbită în cuadripolul de adaptare printr-o manevră anume, astfel încât să fie adaptată numai partea rezistivă a acestora.

Această accepţiune nu este foarte corectă faţă de realitate, dar pentru situaţia traficului de radioamator este acceptabilă.

Adaptarea pe imagini este mult mai complexă şi laborioasă şi nu va fi abordată în acest articol.

Revenind, trebuie ca circuitul de adaptare să asigure un transfer maxim al puterii de la generator la sarcină, în condiţiile unui randament ridicat, ambele condiţii în benzile de frecvenţe alocate serviciului de radioamatori.

Rezumând, vom căuta criteriile de proiectare care s­ă conducăla acest deziderat în cazul unor impedanţe rezistive care trebuie adaptate pentru transfer maxim de putere.

Reţelele de adaptare au configuraţii din cele mai diverse, sunt compuse numai din elemente reactive, bobine şi capacităţi şi au 2 sau 3 poli uzual, mai rar cu mai mulţi poli şi numai când se lucrează pe impedanţe imagini în bandă largă.

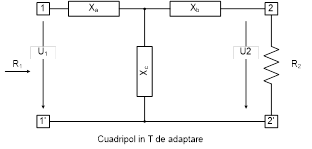
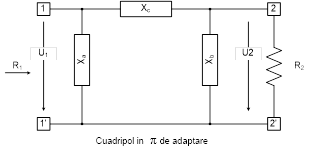
Cele mai uzuale configuraţii, care se regăsesc pe majoritatea transmatch-urilor de unde scurte, sunt reţele în “T” sau “π”.

Fig. 1

3 Calculul reţelelor de adaptare de impedanţe

Aşa cum am menţionat anterior, vom îndrepta calculul acestor reţele pe cazul mai particular cand cele două impedanţe sunt pur rezistive.

Elementele reţelei se dimensionează punând condiţia ca impedanţa de intrare a cuadripolului, când este terminat pe R₂, să fie egală cu R₁.

In vederea stabilirii relaţiilor din care rezultă elementele reţelei, se presupune că la bornele 1-1’ (fig.1) se aplică un generator de rezistenţă R1, care, prin intermediul reţelei, asigură transferul maxim de putere la bornele 2-2’. In această situaţie, rezistenţele R₁ şi R₂ satisfac condiţiile care definesc impedanţele imagini ale cuadripolului.

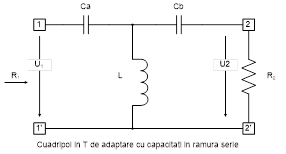
In continuare, vom axa calculul pe reţeaua în “T” de adaptare.

Prin câteva manevre elementare de calcul de electrotehnică, se obţin următoarele expresii care leagă reactanţele X_a, X_b şi X_c de impedanţele R₁ şi R₂.

Fiind date rezistenţele R₁ şi R₂, se pot deduce elementele reţelei de adaptare X_a, X_b şi X_c.

Pe de altă parte, impedanţele imagine ale cuadripolului şi elementele acestuia, satisfac următoarele relaţii:

Z_i1=R₁ şi Z_i2=R₂

Unde

                Z_i1 şi Z_i2 sunt impedanţele imagine ale cuadripolului

                Z_1g şi Z_2g sunt impedanţele în gol ale cuadripolului

                Z₁₂ impedanţa de cuplaj a cuadripolului dintre circuitul de intrare şi cel de ieşire al cuadripolului

In cazul reţelei de adaptare în “T”, se poate scrie

Z₁₂=jX_c; Z_1g=jZ_1g şi Z_2g=jX_2g

Se deduce

După câteva prelucrări matematice se obţine:

Şi, în final rezultă:

Se observă că se obţin două valori pentru X_a şi X_b, după cum se iau semnele plus sau minus.

Cu aceste rezultate, în principiu, reţeaua de adaptare este determinată, dar cu următoarele remarci.

·         Avem două date de intrare, R₁ şi R₂, şi trei variabile, X_a, X_b şi X_c. Rezultă că una din variabile trebuie aleasă după un criteriu anume.

·         Avem o condiţionare impusă de existenţa radicalului, şi anume >0

·         Dacă R₁ este diferit de R₂, cel puţin una din reactanţele X_1g şi X_2g, este mai mică, în valoare absolută decât X_c, de unde rezultă că cel puţin una din reactanţele X_a sau X_b trebuie să fie de semn contrar cu X_c.

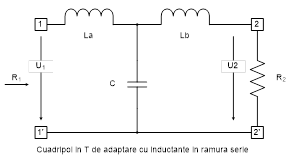
Aşa cum menţionat anterior, vom dezvolta teoria pe cazul unui cuadripol de adaptare în “T”, ca în figura următoare

Configuraţiile prezentate sunt idealizate, în sensul că, în realitate, atât generatorul, cât şi sarcina, prezintă părţi reactive

Pentru a reduce configuraţia reală la cea idealizată se procedează în felul următor

·         Reactanţa X_b se înlocuieşte cu X_b – X₂

·         Reactanţa X_a se înlocuieşte cu X_a – X₁

Se aplică apoi formulele de calcul pentru impedanţele X_a şi X_b.

Rămâne de stabilit criteriul de alegere a reactanţei X_c.

4 Dimensionarea reactanţei de cuplaj

Este evident că, relaţiile dezvoltate anterior au o multitudine de soluţii atâta timp cât X_c poata fi ales arbitrar.

Există o singură condiţie şi anume >0. Chiar şi aşa, câmpul de alegere al impedanţei X_c trebuie îngustat.

Analizând configuraţia relei de adaptare, se constată că aceasta este o structură selectivă, cu rezonanţă la frecvenţa la care se produce adaptarea. Acest lucru este explicabil prin faptul că, în cazul transferului maxim de putere, de la generator la sarcina, energia reactivă stocată în capacităţi şi inductoare, se compensează, rezultând rezonanţa.

Dar, în afara rezonanţei, transferul de putere scade, până la o valoare pe care o acceptăm ca fiind rezonabilă.

O valoare acceptabilă este o pierdere de 10% din puterea maxim disponibilă.

In această situaţie avem relaţia

Pentru o pierdere de 10% din putere se obţin bine cunoscutele valori

Unde

Ρ – coeficientul de reflexie

σ - factorul de unde staţionare

a – pierderea de putere de neadaptare

Cu aceste considerente, am obţinut criteriul de alegere pentru X_c. Din multitudinea de valori pentru Xc se va alege acea valoare pentru care pierderea de putere este de 10%.

Pe de altă parte trebuie să ţinem cont de faptul ca circuitul de adaptare se termina pe impedanţe care conţin şi parte reactivă. Partea reală şi cea imaginară a impedanţei se subînscriu în condiţia |ρ|<0.33.

Pentru a putea dimensiona circuitul de adaptare trebuie determinate domeniile de existenţă ale impedanţei ce urmează să fie adaptată şi care respectă această condiţie. Ne vom ajuta de diagrama Smith şi de proprietăţile ei în această sarcină.

Diagrama Smith este o reprezentare în plan ale părţilor reală şi imaginară ale unei impedanţe prin transformarea conformă:

Această transformare este mai comodă pentru analiza circuitelor electrice de radiofrecvenţă întrucât reduce planul XY la dimensiunea unui cerc.

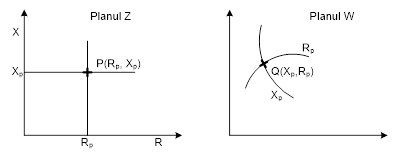
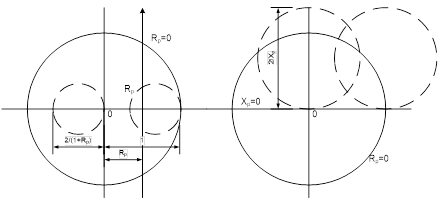
Prin această transformare, dreptele din planul Z se transformă în cercuri în planul W, cercurile în cercuri iar unghiurile se păstrează.

O verticală R=R_p din planul Z descrie un cerc care trece prin origine, are diametrul  şi centrul pe axa R.

O orizontală X=X_p din planul Z descrie un cerc care trece prin origine, are diametrul  şi centrul pe axa X.

Condiţionarea fundamentală care trebuie aflată, şi care determină existenţa circuitului de adaptare, este de determina domeniul de existenţă pentru Z₁ şi Z₂ în condiţia unui coeficient de reflexie maxim admisibil.

Coeficientul de reflexie se alege admiţând o pierdere de putere prin neadaptare.

Se demostrează că valorile pentru R şi X, care verifică această condiţie, se află cuprinse în cercul de ρ constant de pe diagrama Smith. Acesta are centrul la (R=1, X=0) şi diametrul egal cu modulul lui ρ.

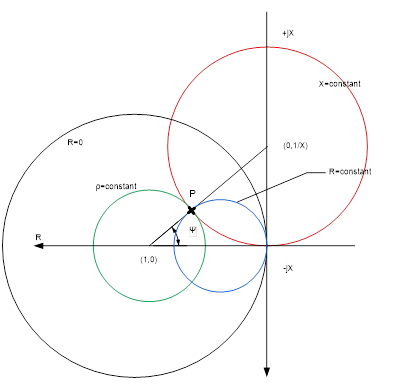
Reprezentarea acestei situaţii este în figura următoare:

Partea rezistivă a impedanţei este evident mai mare decât  şi mai mare decât σ.

Partea imaginară, care se sunînscrie pe cercul roşu, de valoare constantă, trebuie să fie mai mică, în modul, decât valoarea determoinată de punctul P, tangenta între cercul ρ=constant şi cercul X=constant.

Cu câteva calcule de geometrie analitică se obţin următoarele rezultate importante:

Altfel spus, pentru un domeniu de adaptare mai mic decăt coeficientul de reflexie, impedanţele terminale care pot fi adaptare trebuie să respecte cele două relaţii.

Prin măsurători efectuate asupra circuitului de antenă, se determina valorile R_p şi X_p, în cadrul benzii de lucru şi astfel, cu relaţiile precedente, se determină factorul de unde staţionare şi coeficientul de reflexie maxim admisibile.

Plaja de variaţie a impedanţei care trebuie să fie adaptată se mai poate micşora ţinând seama de faptul că reţeaua de adaptare, împreună cu impedanţa terminală, sunt circuite selective, caracterizate de o frecvenţă de rezonanţă şi un factor de calitate. Expresia generală a impedanţei este , unde

 reprezintă dezacordul generalizat iar Q factorul de calitate al reţelei de adaptare împreună cu rezistenţele terminale.

Dacă punem condiţia ca reţeaua de adaptare să asigure o funcţionalitate de cel puţin |ρ|<0.33 echivalent cu σ<2 avem

Unde, R_n este partea rezistivă a impedanţei normata la R₀.

Rezonanţa circuitului împreună cu adaptarea înseamnă R_n=1. In această presupunere, expresia se simplifică la următoarea formă:

De unde se deduce

Această relaţie relevă faptul că, pentru o valoarea asumată a coeficientului de reflexie, ρ, din considerente energetice, între dezacordul generalizat, β, şi factorul de calitate, Q, există o interdependenţă şi anume:

Bandă de Adaptare Mai Mare Presupune un Factor de Calitate mai Mic

Cu această ultimă relaţie, s-a încheiat practic analiza privind modul de dimensionare a reţelei de adaptare în “T”. Relaţii similare se obţin şi pentru reţeaua de adaptare în “π”.

Impunând un coeficient de reflexie şi o bandă de frecvenţă prin dezacordul generalizat, β, se determină valoarea maximă pentru factorul de calitate Q, care, împreună cu formulele ce definesc reactanţele reţelei, determină valoarea limită a reactanţei de cuplaj X_c.

In următorul capitol se va aplica această metodologie pentru dimensionarea reţelei de adaptare a unei antene filare în configuraţie “V întors” .

 5 Date limită în benzile de unde scurte

Analiza din acest articol s-a concentrat pe benzile de frecvenţă utilizate în traficul de radioamatori. Am ales această limitare deoarece circuitul de adaptare este destinat acestor benzi şi prin urmare o extindere a gamei de frecvenţe de lucru poate conduce la valori ale componentelor reţelei de adaptare care nu sunt utile.

Trecând în revistă date benzilor de radioamatori, prezint în tabelul următor, benzile de frecvenţe alocate în regiunea 1 IARU, frecvenţele centrale şi benzile ocupate necesare de emisiuni.

Frecvenţa centrală a fost asumată ca media geometrică a limitelor benzii alocate astfel:

In tabelul următor se prezintă valorile dezacordului generalizat şi pierderea de putere prin reflexie pentru o gamă a coeficientului de unde staţionare care pot apărea în traficul real

unde

·          este dezacordul generalizat maxim admisibil pentru cazul unei impedanţe selective, care trebuie adaptate, şi pentru un coeficient de unde staţionare asumat

·         este pierderea de putere prin neadaptare pentru un coeficient de unde staţionare asumat

Vom continua analiza pentru situaţia unui coeficient de unde staţionare σ=2 care corespunde unei pierderi de putere de 11%. Această alegere are semnificaţia ca dacă reţeaua de adaptare este în aşa fel calculată încât să prezinte o neadaptare de σ=2 la capetele benzii, nu mai este nevoie de un acord suplimentar acceptând o pierdere a puterii emise de 11%. Se poate arăta că această pierdere nu influenţează semnificativ calitatea emisiunii şi distanţa de legătură.

Aşa cum am prezentat anterior, valorile impedanţei care trebuie adaptate, partea rezistivă şi cea reactivă, se înscriu în cercul de ρ=constant de pe diagrama Smith. In tabelul următor sunt prezentate limitele acestor valori pentru σ=1.5÷5.

Si o ultimă relaţie de limitare, derivată din analiza anterioară, este

Se observă că aceste relaţii de limitare nu sunt legate de banda de lucru, sunt condiţionate de coeficientul de unde staţionare, de lărgimea de bandă  propusă a fi acoperită şi de arhitectura reţelei de adaptare.

6 Un exemplu de caz

Am aplicat această procedură de calcul la realizarea unui circuit de adaptare pentru o antenă simplă V-întors acordată pentru banda de 40 m.

Scopul este de a realiza o reţea de adaptare care să acopere întreaga gamă de frecvenţe, pe subbenzi, fără acord suplimentar înn cadrul aceteia.

Primul pas a fost măsurarea impedanţei antenei cu ajutorul unui vector voltmetru ăn banda 1.8 – 30 MHz.

Rezultatele sunt cuprinse în tabelul următor:

Trebuie să menţionez că masurătoarea a fost făcută la capătul fiderului de antenă cu o lungime electrică de 18.6 m. Fiderul roteşte valoarea impedanţei antenei pe diagrama Smith astfel că la capătul fiderului se va măsura altă valoare. Acest lucru nu contează întrucât adaptorul se montează la intrarea în staţie.

O trecere în revistă a condiţiilor pentru care adaptarea este opţională este următoarea:

Examinând tabelul cu măsurătorile antenei se observă  că doar în banda de 7 MHz se întrunesc condiţiile pentru care, fără o reţea de adaptare, pierderea de putere este sub 10%, în rest, fiind nevoie de ajutorul adaptării pentru a aduce antena în zona de acceptabilitate.

Procedura de calcul este următoarea:

·         Se măsoară impedanţa antenei în banda aleasă cu ajutorul unui voltmetru vectorial gen NanoVNA. R₁ este partea reală iar X₁ partea imaginară a impedanţei

·         Se stabileşte lărgimea de bandă a reţelei de adaptare astfel încât să acopere banda alocată de ANCOM. Se ia o margine de rezervă de 10% pentru acoperirea toleranţelor pieselor din montaj

·         Se calculează reactanţele reţelei de adaptare în T, X_a şi X_b reactanţele condensatoarelor, pentru o valoare aleasă a lui X_c, reactanţa bobinei. Se calculează pentru mai multe valori X_c, până când se obţine lărgimea de bandă dorită.

·         Cu ajutorul unui program de analiză de circuit cum ar fi LTSpice, MicroCap, RFSim 99, determină lărgimea de bandă pentru care reflexia este ρ<0.33 (σ<2)

·         Se absoarbe partea imaginară a impedanţei antenei, X₁, în valoarea reactanţei X_a

Cu acestea, calculul s-a terminat, toate elementele reţelei de adaptare sunt determinate.

Urmează o simulare cu unul din programele menţionate pentru a verifica funcţiile reţelei şi pentru a determina prin calcul tensiunile şi curenţii din circuit la puterea maximă.

Se realizează montajul şi se compară măsurătorile cu valorile simulate.

Mihai Stocec

August 2023

Erată şi Anexa tehnică (adaugate la 23.08.2024)

Erată

Expresia corectă:

Anexa tehnică

1)      Expresia corectă a dezacordului generalizat, β, este:

, unde

- ω este notată pulsaţia curentului

- f este frecvenţa curentului

Între cele două mărimi există relaţia

“f₀ “ este frecvenţa centrală a benzii de analiză, şi este în acelaşi timp frecvenţa de rezonanţă a circuitului asimilat pentru antenă. Pentru abateri mici faţă de frecvenţa de rezonanţă, se poate folosi pentru dezacordul generalizat expresia aproximativă

, unde .  Pentru o abatere de 10%, eroarea la nivel de  este de circa 4%, deci acceptabilă.

In cadrul acestor notaţii, banda de lucru a circuitului rezonant asimilat antenei este simetrică faţă de , şi este

2)      Lungimea fiderului nu are importanţă, intrucât analiza se referă la adaptarea la capătul de jos al fiderului, acolo unde se montează cutia de adaptare. Referirea în text a fost făcută cu scopul de a atrage atenţia cititorului că la capătul de jos al fiderului se măsoară o impedanţă diferită faţă de cea a antenei. Aceasta poate fi aflată prin inginerie inversă, dacă se cunoaşte lungimea electrică a fiderului care se poate afla fie cunoscând lungimea fizică şi coeficientul de velocitate, fie, prin masurători. In cazul studiului de caz am preferat masurătoarea primei rezonanţe paralel, cu capătul dinspre antenă în gol. Rezonanţa se produce cand lungimea electrică a fiderului este egală cu un sfert din lungimea de undă.

3)      In concluzie, trebuie reţinut faptul că această analiză a fost făcută pentru ansanblul fider + antenă, dar este valabilă pentru orice structură care, pe porţiuni, poate fi asimilată cu una selectivă, având o rezonanţă. Mihai Stocec

Mihai Stocec

August 2024

ing. Mihai Stocec YO3AYX

Articol aparut la 21-8-2024

1204