 |
|
|
Linii de transmisieTraducere si adaptare: Valericã Costin YO7AYH
Traducere si adaptare a articolului "Transmision Lines" ap?rut în "The Radio
Amateur’s Handbook", editia 1978, pag. 573 la 576, realizat? de Valeric? Costin YO7AYH
Liniile de transmisie si teoria pe care se bazeaz? joac? un rol important în multe faze
ale comunicatiilor. Aceasta se datoreaz? faptului c? principiile de baza pot fi
aplicate la o mare diversitate de probleme. Tipurile de linii de transmisie includ
configuratii simple din dou? conductoare ca panglica TV (dou?
conductoare paralele) si cablul coaxial. Astfel de linii sunt cele mai
utilizate în domeniul frecventelor radio si pot fi folosite chiar pân? la
domeniul microundelor. Linii de transmisie si circuite O linie de transmisie difer? de un circuit ordinar printr-un aspect foarte
important. Într-un circuit cu componente discrete nu se simt efectele de îintarziere
care apar la popagarea energiei electromagnetice, cu vitez? finit?, printr-o
linie de transmisie, pentru c? dimensiunile componentelor din circuit sunt in
mod normal mici in comparatie cu lungimile de und? ale oric?rei frecvente
prezente în circuit. Aceast? afirmatie nu este valabil? în cazul liniilor de transmisie. Timpul finit de propagare
prin liniile de transmisie devine un factor de important? crucial?. Acest fapt
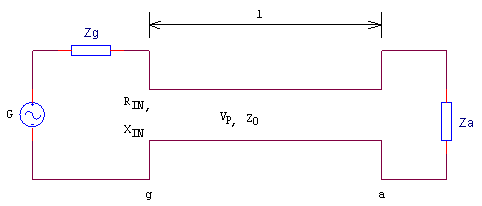
poate fi ilustrat cu ajutorul figurii 1. În Fig.1 linia de transmisie separ? sursa de sarcin?. Limita sursei este in
punctual "g", iar limita antenei este în punctual "a". Distanta dintre surs? si
anten? este "l". În cazul unei linii de transmisie uniform? (aceeasi form? a
conductorului în orice sectiune transversal? a liniei) sunt necesari numai doi
parametri ca s? exprime complet proprietatile liniei. Acestia sunt viteza de
faza
Dac?
se consider? c? linia nu are pierderi, atunci impedanta caracteristic? a liniei
S?
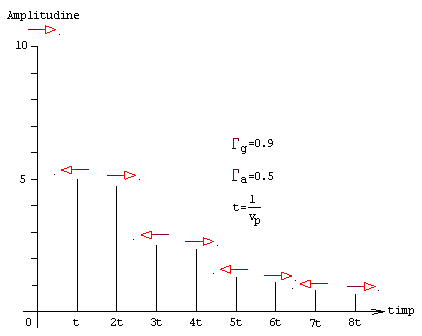
presupunem c? sursa va emite putere c?tre anten? pe o durat? foarte scurt?
(short burst). Aceasta este reprezentat? de linia vertical? de 10 unit?ti din
seria de linii reprezentate in Fig.2. Când
pulsul de tensiune ajunge la impedanta de sarcin? Acest
proces de dute-vino va dura teoretic un timp infinit, dar practic, dup? câteva
reflexii, intensitatea undelor devine foarte mic?. Dac? în loc de o emisiune
scurt? se va aplica la intrarea liniei de transmisie o tensiune de
radiofrecventa cu durata mai mare, atunci tensiunea într-un punct al liniei
(tensiunea dintre cele dou? conductoare ale liniei, în punctul respectiv de pe
linie) va consta din suma tensiunilor undelor care c?latoresc spre dreapta (c?tre
anten?) si a tensiunilor undelor care c?l?toresc spre stânga (undele reflectate
de anten?). Suma total? a undelor care c?l?toresc spre dreapta este numit? unda
directa sau unda incident?, în timp ce suma total? a undelor care
c?l?toresc spre stanga este numit? unda reflectat?. Dac? vor fi
indeplinite anumite conditii referitoare la impedanta de sarcin? Ecuatii
si factori de linie Deoarece
liniile de transmisie sunt uzual conectate între circuite cu parametri concentrati
sau între circuite discrete, este convenabil s? se exprime impedanta de
intrare a unei linii in functie de impedanta de iesire sau de sarcin?. O
linie privit? în acest fel este similar? cu un filtru sau cu un circuit de
adaptare cu o impedant? de sarcin? dat?. Când
se aplic? asemenea relatii este foarte important s? se tin? cont de modul în
care sursa si sarcina sunt conectate la linie. Totdeauna sunt niste efecte
parazite care apar datorit? conectorilor si din configurarea circuitelor post
conector. Acestea pot cauza ca linia sa "vad?" o impedant? diferit? decât cea
rezultat? prin masur?tori efectuate direct la terminalele sarcinii. Acest lucru
este sugerat în Fig.1 prin schimb?rile bruste ale dimensiunii liniei in
punctele "g" si "a". Chiar dac? linia scurt? care conecteaz? generatorul la
linia principal? de transmisie (si cea care conecteaz? sarcina la linie) are
aceeasi impedant? caracteristic? ca a liniei de transmisie, dar dac? m?rimea
este diferit?, atunci va apare o neadaptare. În mod normal acest efect poate fi
neglijat la hf dar devine important dac? frecventa ajunge pân? în domeniul vhf
sau mai sus. Revenind
la cele discutate în Fig.2, se poate defini coeficientul de reflexie în
tensiune. Acesta se noteaz? cu una dintre literele grecesti unde: Legatura
dintre rezistenta de radiatie a antenei Dac?
În
cazul în care nu sunt reflexii de la sarcin?, atunci distributia tensiunii
dealungul liniei este constant?, sau "plat?". În situatia în care exist?
reflexii, atunci distributia tensiunii dealungul liniei nu va mai fi constant?,
ci vor exista puncte în care tensiunea va fi maxim? si puncte în care tensiunea
va fi minim?. În aceast? situatie vor exista unde stationare pe linie. Raportul
dintre tensiunea maxim? de pe linie si tensiunea minim? de pe linie (cu conditia ca linia s? fie mai lung? decât un
sfert de lungime de und?) este definit ca raport de unde
stationare în tensiune (voltage standing-wave ratio) si se noteaz? cu
VSWR, sau simplu SWR. De
aici rezult? Legatura
dintre (Se
demonstreaz? c?: Aceast?
definitie a raportului de unde stationare în tensiune este mai general? si este
valabil? pentru orice lungime de linie. Adesea
nu se cunoaste valoarea impedantei de sarcin?. În aceast? situatie coeficientul
de reflexie în tensiune se exprim? prin urmatoarea relatie: unde
Puterile
direct? si reflectat? sunt usor de masurat cu watmetre disponibile pe piat? sau
cu watmetre construite de radioamatori. Totusi este evident c? dac? se
utilizeaz? relatia anterioar? nu pot exista alte surse de putere la sarcina.
Pentru exemplu, in Fig.2 este mentionat c? coeficientul de reflexie în tensiune
al generatorului este Din
fericire este posibil s? se determine rezistenta si reactanta unei linii
terminate cu o sarcin?, dac? rezistenta si reactanta sarcinii sunt cunoscute si
dac? mai sunt cunoscute lungimea liniei si impedanta caracteristic? a ei. (În
cazul liniilor reale trebuie s? se tin? cont de factorul de velocitate al
liniei). Se
fac urmatoarele notatii: Cu
notatiile de mai sus se demonstreaz? c? impedanta relativ? complex? (scris? în
planul complex) la intrarea în cablu este data de relatia: Din
relatia pentru unde
Expresiile
pentru Se
reaminteste c? Ecuatiile
mentionate mai sus pentru Pentru
o linie f?r? pierderi, cu impedanta caracterisitc? În
formulele pentru Pentru
cei c?rora li se pare dificil s? se lucreze cu ecuatiile pentru În
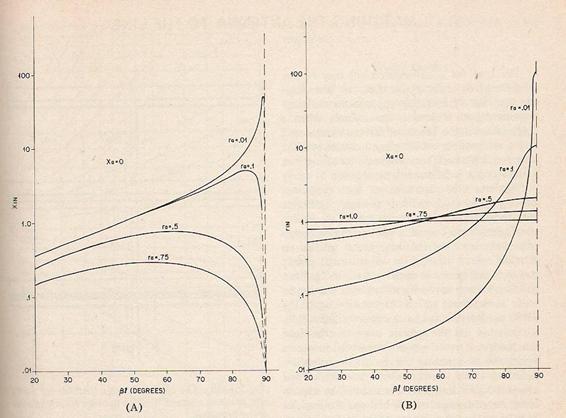
Fig. 3A sunt prezentate curbele lui Ca
s? putem afla valorile lui Astfel: (15) Dac?
lungimea fizic? a liniei de alimentare este Când
aceast? valoare a lui Dac?
Se
obtine astfel formula pentru un transformator în sfert de lungime de und?: Pentru
Destul de des se presupune în mod gresit c? puterea reflectat? de o sarcina este într-un fel o putere pierdut?. Aceast? afirmatie este adevarat? numai dac? linia de transmisie are pierderi considerabile si puterea este disipat? pe drumul de întoarcere de la sarcin? la surs?. Pe de alt? parte, transformatorul în sfert de lungime de und? este un exemplu unde reflexiile pe o linie f?r? pierderi pot fi utilizate în mod practic la adaptarea dintre impedanta de sarcin? si impedanta sursei care este diferit? de cea a sarcinii. Dac?
lungimea fizic? a liniei de alimentare este
Cu
Rezultatele
din ecuatiile (19) arat? c? dac? se foloseste o lungime fizic? de cablu egal?
cu o jum?tate de lungime de und? ( Dac?
linia se termin? pe o rezistent? egal? cu zero, atunci si rezistenta de intrare
Dac?
în plus lungimea fizic? a cablului de alimentare este o jum?tate de lungime de
und?, sau multiplu de jum?tate de lungime de und?, În
cazul special în care reactanta cu care se termin? linia este zero, În
cazul special în care reactanta cu care se termin? linia este infinit,
si
se înlocuieste valoarea lui
Deci
cazurile speciale în care reactanta cu care se termin? linia este fie zero, fie
infinit (mentinându-se valoarea zero a rezistentei antenei
O lungime scurt? de linie, cu un scurtcircuit la cap?tul dinspre sarcin? apare ca o inductant?, în timp ce o linie deschis? apare ca o capacitate. Ca sarcin? a unei linii de transmisie poate fi orice dispozitiv (element) capabil s? disipe putere de radio frecvent?. Cel mai utilizat tip de sarcin? conectat? la o linie de transmisie este antena. Când o linie de transmisie este conectat? între o anten? si un receptor, sarcina o constituie intrarea în receptor (nu antena), pentru c? puterea este luat? de la o und? trecatoare, care loveste antenna, si livrat? receptorului. Conditiile
existente la sarcin?, si numai sarcina, determin? raportul de unde stationare
pe linie, indiferent de aplicatie. Dac? sarcina este pur rezistiv? si egal? în
valoare cu impedanta caracteristic? Numai în câteva cazuri speciale valoarea sarcinii se potriveste (adapteaz?) cu a liniei de transmisie. În toate celelalte cazuri este necesar fie s? se opereze (lucreze) cu o neadaptare si s? se accepte valoarea SWR-ului, fie s? se ia m?suri pentru a se face adaptarea între linie si sarcin? cu ajutorul unor transformare sau dispozitive similare. Transformatoarele adaptoare de impedant? pot lua o varietate de forme fizice, depinzând de circumstante. Dac? se doreste ca SWR-ul s? fie mentinut cât mai mic posibil, atunci este esential ca sarcina la punctual de conexiune cu linia de transmisie s? fie pur rezistiv?. În general acest lucru presupune ca sarcina s? fie acordat? la rezonant?. Dac? sarcina îns?si nu este rezonant? pentru frecventa de lucru atunci uneori acordarea poate fi realizat? în sistemul de adaptare.
Nota traducatorului 1. Din cele prezentate anterior se constat? c? raportul de reflexie în tensiune este dat de doua formule:
Pentru
cazul din Fig.2, unde este specificat c? Tot pentru cazul din Fig.2 se poate afla si raportul de unde stationare:
De
obicei nu se cunoaste coeficientul de reflexie în tensiune, ci se cunoaste
raportul de unde stationare, care este m?surat cu un reflectometru. Din relatia
Având
valoarea coeficientului de reflexie în tensiune se poate afla cât din puterea
direct? va fi reflectat? de antenna: Pe baza celor expuse mai sus a fost întocmit tabelul 1. În
tabelul 1 s-a considerat c? atunci când se etaloneaz? un reflectometreu se fac
reglajele astfel încât pe pozitia "directe" indicatia instrumentului s? fie
100%, adic? valoarea 1. Evident, pe pozitia "reflectate", instrumentul arat? o
valoare mai mic? decât 1 (pentru exemplu 0.1, sau 0.3, sau 0.5, etc). De aceea
în tabel, în coloana Tabelul 1 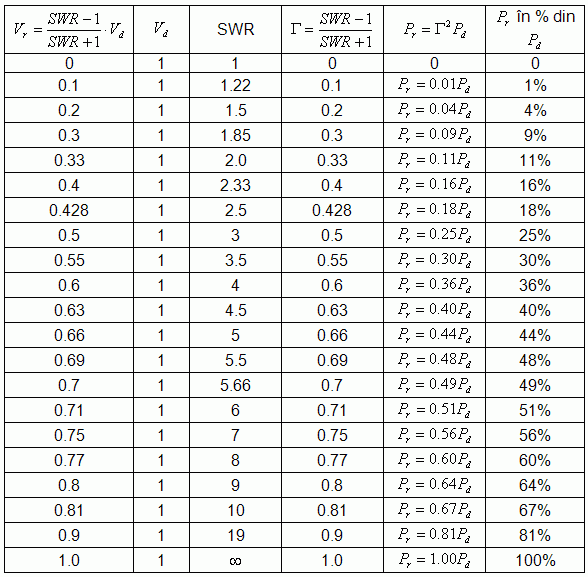 Cu ajutorul tabelului 1 se pot grada instrumentele de m?sur? (microampermetre, sau miliampermetre) ale reflectometrelor astfel încât s? indice direct raportul SWR de unde stationare. Pe
baza datelor din tabelul 1 se poate trasa un graphic, Fig.4, care s?
arate, în ordonat?, valoarea raportului de unde stationare în tensiune, SWR si
pe abscis? valoarea relativ? în procente a tensiunii reflectate,
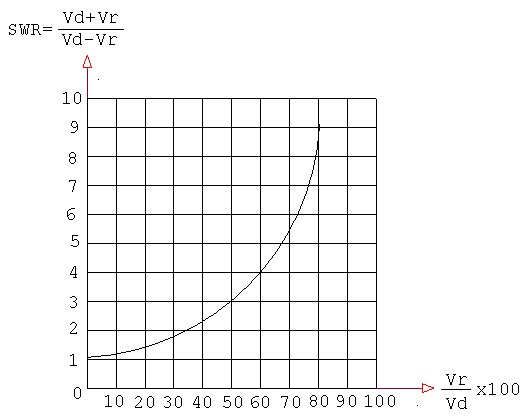 Fig. 4 Curba raportului de unde stationare SWR în functie de valoarea relativ? în procente a tensiunii reflectate. Dac?
se cunoaste raportul de unde stationare SWR si se doreste s? se afle valoarea
tensiunii reflectate, atunci graficul din Fig.4 se poate inversa, astfel încât
în abscis? s? fie SWR si în ordonat?
 Fig. 5 Curba tensiunii reflectate relative în functie de raportul de unde stationare.
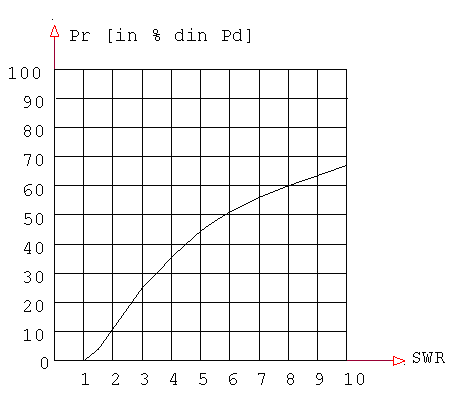 Fig. 6 Curba puterii reflectate Pr, în functie de raportul de unde stationare SWR. Puterea reflectat? Pr este reprezentat? în procente din puterea direct? Pd
Pd = puterea în unda direct? (puterea aplicat? la intrarea în linie);
2. Dac? raportul de unde stationare pe linia de transmisie nu poate fi schimbat prin nici-un reglaj efectuat la intrarea în linie, atunci la ce ajut? cuplorul de anten? (transmach-ul, sau antena tuner)?

Fig. 7 Schema de conectare a cuplorului de anten? la emit?tor Cuplorul de anten? se amplaseaz? între emit?tor si intrarea în linie. Utilizarea cuplorului de anten? face ca pe segmentul de linie dintre el si emit?tor s? nu existe unde reflectate (sau, în anumite cazuri, s? existe un minim de unde reflectate, indicate de SWR1). În aceast? situatie curentul furnizat de etajul final al emit?torului va fi minim, protejându-se astfel etajul final de curenti excesivi, iar puterea transmis? de emitator spre anten? va fi maxim?, datorit? adapt?rii dintre impedanta de iesire a emit?torului si impedanta de intrare în linia de alimentare. Eliminarea undelor reflectate pe segmentul de linie dintre emit?tor si cuplorul de anten? nu înseamn? si eliminarea undelor reflectate de pe linia existent? între cuplor si anten?. Acest lucru poate fi dovedit cu un alt reflectometru (SWR2) instalat între cuplor si anten?. Daca antena este pur rezistiv? (f?r? componente reactive) si dac? valoarea rezistentei de radiatie este egal? cu valoarea impedantei caracteristice a liniei f?r? pierderi, atunci pe linie nu vor fi unde reflectate (deci nu vor fi unde stationare) si cel de al doilea reflectometru va indica lipsa lor. În toate celelalte cazuri, când antena nu este pur rezistiv? si are si componente reactive, iar impedanta antenei va diferi de impedanta caracteristica a liniei, vor exista unde reflectate care, vor conduce la existenta undelor stationare pe linie. În concluzie, un cuplor de anten? nu va elimina undele stationare existente pe linie, datorit? neadaptarii dintre anten? si linia de transmisie. El va ajuta la reducerea curentului debitat de etajul final, protejând tranzistorii sau tuburile electronice din etajul final de curenti excesivi, si va face posibil s? se transfere maximum de putere de la emitator spre anten?. Reprinted with permission of the American Radio Relay League (ARRL). Copyright © ARRL
Articol aparut la 7-12-2005 29632 Inapoi la inceputul articolului | |
|
Comentariul trebuie sa se refere la continutul articolului. Mesajele anonime, cele scrise sub falsa identitate, precum si cele care contin (fara a se limita la) atac la persoana, injurii, jigniri, expresii obscene vor fi sterse iar dupa caz se va ridica dreptul de a posta comentarii.
| |||||
Opiniile exprimate în articole pe acest site aparţin autorilor şi nu reflectă neapărat punctul de vedere al redacţiei.
|
Copyright © Radioamator.ro. Toate drepturile rezervate. All rights reserved
Articole | Concursuri | Mica Publicitate | Forum YO | Pagini YO | Call Book | Diverse | Regulamentul portalului | Contact |
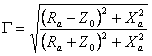 (2)
(2)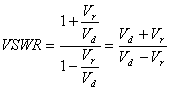 ) (6)
) (6)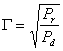 (7)
(7)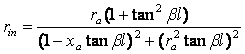 si (9)
si (9)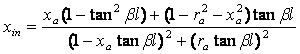 (10)
(10)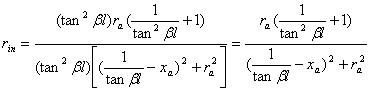 (14)
(14)
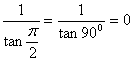 si
si 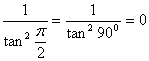 . Având în vedere
aceste valori, ecuatiile liniilor de transmisie pentru
. Având în vedere
aceste valori, ecuatiile liniilor de transmisie pentru 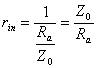
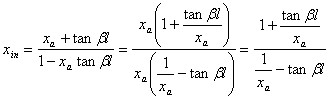 (22)
(22)