Bibliografie:
Bazele Electrotehnicii, Editura didactic? si pedagogic?-1982, autor:
Prof. dr. ing. CONSTANTIN ŞORA
În
figura 1 este reprezentat un receptor (sarcin?) conectat la un generator. Se
pune problema g?sirii conditiilor pe care trebuie s? le îndeplineasc?
receptorul astfel încât s? absoarb? un maxim de putere activ? de la generator.
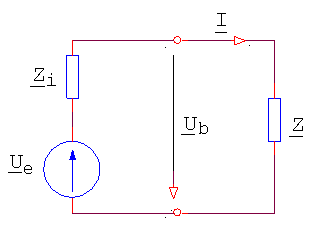
Fig.1 Un receptor conectat la un generator
Notatii:
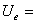 valoarea
efectiv? a tensiunii electromotoare a generatorului, [V];
valoarea
efectiv? a tensiunii electromotoare a generatorului, [V];
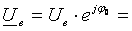 expresia
în planul complex a tensiunii efective electromotoare
expresia
în planul complex a tensiunii efective electromotoare
a generatorului, [V];
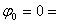 unghiul
dintre vectorul tensiunii electromotoare si axa real?, [rad, sau
unghiul
dintre vectorul tensiunii electromotoare si axa real?, [rad, sau
grade]. S-a considerat 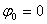 ,
adic? tensiunea electromotoare se va reprezenta în axa real?.
,
adic? tensiunea electromotoare se va reprezenta în axa real?.
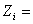 modulul
(valoarea absolut?) a impedantei interne a generatorului, [
modulul
(valoarea absolut?) a impedantei interne a generatorului, [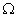 ];
];
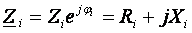 =
expresia în planul complex a impedantei interne a
=
expresia în planul complex a impedantei interne a
generatorului, [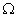 ];
];
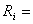 rezistenta
intern? a generatorului, [
rezistenta
intern? a generatorului, [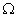 ];
];
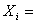 reactanta
intern? a generatorului, [
reactanta
intern? a generatorului, [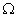 ];
];
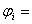 unghiul
dintre impedanta
unghiul
dintre impedanta 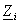 si
rezistenta
si
rezistenta 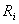 ,
[rad, sau grade];
,
[rad, sau grade];
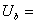 valoarea
efectiv? a tensiunii de la bornele generatorului, [V];
valoarea
efectiv? a tensiunii de la bornele generatorului, [V];
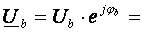 expresia
în planul complex a tensiunii efective de la bornele
expresia
în planul complex a tensiunii efective de la bornele
generatorului, [V];
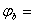 unghiul
dintre axa real? si vectorul tensiunii de borne, [rad, sau grade];
unghiul
dintre axa real? si vectorul tensiunii de borne, [rad, sau grade];
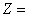 modulul
(valoarea absolut?) a impedantei de sarcin?, [
modulul
(valoarea absolut?) a impedantei de sarcin?, [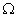 ];
];
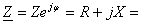 expresia
în planul complex a impedantei de sarcin?, [
expresia
în planul complex a impedantei de sarcin?, [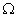 ];
];
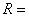 rezistenta
sarcinii, [
rezistenta
sarcinii, [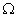 ];
];
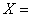 reactanta
sarcinii, [
reactanta
sarcinii, [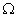 ];
];
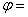 unghiul
dintre impedanta
unghiul
dintre impedanta 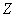 a
sarcinii si rezistenta
a
sarcinii si rezistenta 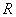 a
sarcinii, [rad, grade];
a
sarcinii, [rad, grade];
Se
consider? generatorul (sursa) de tensiune electromotoare 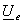 prezentat
în Fig.1. Pentru simplificarea calculelor se consider? c? tensiunea
electromotoare
prezentat
în Fig.1. Pentru simplificarea calculelor se consider? c? tensiunea
electromotoare 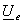 este
reprezentat? în axa real?, adic? unghiul
este
reprezentat? în axa real?, adic? unghiul 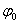 dintre
vectorul
dintre
vectorul 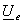 si
axa real? este zero. În acest caz se poate scrie:
si
axa real? este zero. În acest caz se poate scrie:
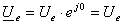 (1)
(1)
Generatorul
are impedanta intern?,
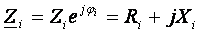 . (2)
. (2)
La
bornele generatorului este conectat un receptor (consumator) caracterizat prin
impedanta:
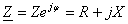 (3)
(3)
Curentul
stabilit în circuit este dat de relatia:
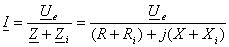 (4)
(4)
Ca
s? se obtin? modulul 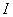 al
curentului (valoarea absolut? a valoarii efective a curentului) vor trebui
f?cute manipul?ri matematice succesive:
al
curentului (valoarea absolut? a valoarii efective a curentului) vor trebui
f?cute manipul?ri matematice succesive:
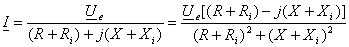 (5)
(5)
Tinând
cont de expresia (1) si separând partea real? de partea imaginar? se obtine:
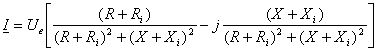 (6)
(6)
Modulul
curentului rezult? usor si este dat de expresia (7):
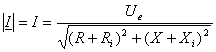 (7)
(7)
P?tratul
valorii efective a curentului este:
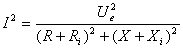 (8)
(8)
Puterea
activ? consumat? de sarcin? este dat? de relatia:
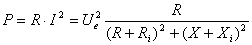 (9)
(9)
Din
expresia (9) se vede c?, în raport cu 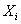 puterea
activ? consumat? de sarcin?, respectiv transferat? de generator sarcinii, este
maxim? dac? (
puterea
activ? consumat? de sarcin?, respectiv transferat? de generator sarcinii, este
maxim? dac? (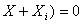 ,
respectiv dac?
,
respectiv dac?
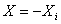 (10)
(10)
Tinând
seama de conditia exprimat? de relatia (10), espresia puterii active devine:
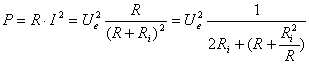 (11)
(11)
Puterea
consumat? de sarcin? este maxim? dac? numitorul din expresia (11) are valoare
minim?. Numitorul acestei expresii este minim dac? 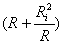 este
minim. Produsul celor doi termeni din suma
este
minim. Produsul celor doi termeni din suma 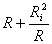 este
constant,
este
constant, 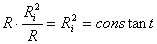 .
În acest caz suma lor este minim? dac? termenii sunt egali, adic?:
.
În acest caz suma lor este minim? dac? termenii sunt egali, adic?:
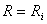 (12)
(12)
Se
constat? c? sunt dou? conditii pentru ca puterea transmis? de generator c?tre
sarcin? s? fie maxim?, conditiile (10) si (11), sau:
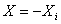 si
si
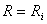 (13)
(13)
Conditiile
obtinute pot fi scrise si sub form? complex?:
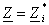 ,
respectiv
,
respectiv 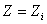 si
si
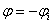 (14)
(14)
unde
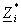 este
expresia conjugat? a impedantei interne
este
expresia conjugat? a impedantei interne 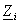 a
generatorului, adic?:
a
generatorului, adic?:
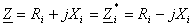 (15)
(15)
Deci
puterea transmis? pe la borne unui receptor este maxim? dac? impedanta complex?
a acestuia este egal? cu conjugata impedantei complexe interioare a
generatorului la bornele c?ruia este conectat.
În
figura 2 este ar?tat? relatia dintre impedanta receptorului si impedanta
intern? a generatorului în conditia de adaptare.
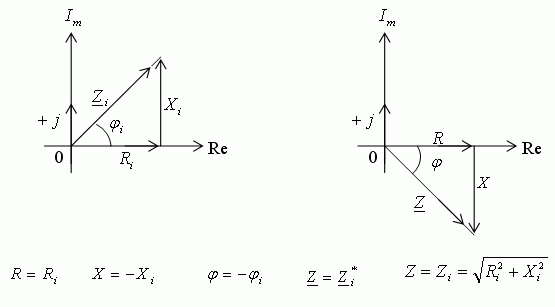
Fig.2
Relatiile dintre impedanta intern? a generatorului si impedanta receptorului la
conditiile de adaptare.
Conditiile
g?site pentru adaptare se exprim? în cuvinte astfel:
Pentru
ca o sarcin? s? absoarb? maximum de putere activ? de la un generator trebuie ca
rezistenta sarcinii s? fie egal? cu rezistenta intern? a generatorului, iar
reactanta sarcinii s? fie egal? si opus? cu reactanta intern? a generatorului;
dac? reactanta intern? a generatorului este inductiv?, atunci reactanta
sarcinii trebuie s? fie capacitiv? si invers, dar ambele s? aib? aceeasi
valoare absolut?. Se spune c? receptorul este adaptat cu generatorul din punct
de vedere al puterii maxime.
Dac?
în relatia (11) se pune conditia 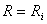 se
obtine valoarea puterii maxime transmis? de la generator la receptor (sarcin?):
se
obtine valoarea puterii maxime transmis? de la generator la receptor (sarcin?):
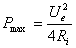 (16)
(16)
În
cazul adapt?rii (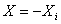 si
si 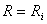 ),
puterea total? în circuit este
),
puterea total? în circuit este
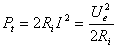 (17)
(17)
Randamentul
corespunz?tor transferului maxim de putere este
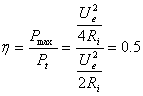 (18)
(18)
Pentru
adaptarea receptorului (sarcinii) la generator se folosesc transformatoare de
adaptare.


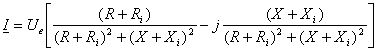 (6)
(6)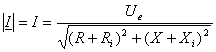 (7)
(7)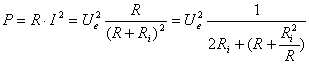 (11)
(11)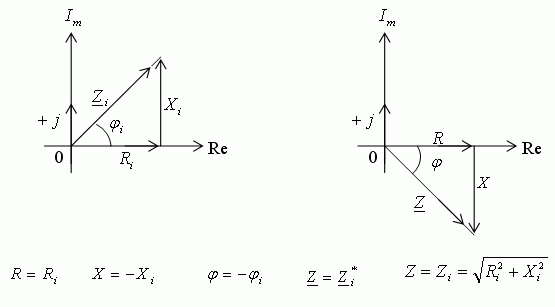
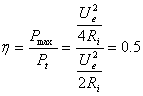 (18)
(18)