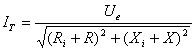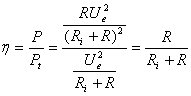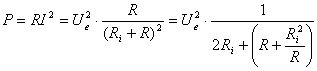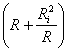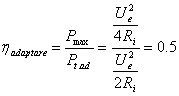Anul
trecut am scris articolul "Teorema transferului maxim de putere activ?",
articol care a ap?rut pe www.radioamator.ro
înainte de atacul care a avut loc asupra acestui sait. De aceea, comentariile asupra acestui articol s-au
pierdut. Unele dintre comentarii au fost foarte "acide". Cu unii dintre cei
care au f?cut comentariile respective am continuat s? corespondez prin e-mail.
Am încercat s? dau r?spunsuri la întreb?rile puse, dar probabil nu am convins.
De aceea m-am hot?rât s? rescriu un articol despre acelasi subiect. Pentru c?
în articolul precedent am utilizat scrierea în forma complex? a m?rililor
sinusoidale si am fost "criticat", în acest articol am utilizat scrierea în
domeniul real si probabil c? voi fi din nou criticat.
Am c?utat pe internet articole cu continut asem?n?tor. Cel care mi-a pl?cut în mod deosebit se intituleaz? "Output
impedance and maximum power transfer", scris de Dr. David
Knight-G3YNH, articol care poate fi g?sit la urm?toarea adres?: http://www.g3ynh.info/zdocs/AC_theory/part_4.html#1-28#1-28
.
Trebuie s? recunosc c? ideea reprezent?rii grafice a puterilor care se
disip? în circuitul analizat (graficele din paragraful 3 a acestui articol) am
luat-o din articolul mentionat mai sus, scris de G3YNH.
Paragraful 4 al acestui articol, intitulat
"Concluzii", este tradus integral din articolul Dr. David Knight. Pentru
publicarea acestui paragraf am primit acceptul de la Dr. David Knight.
1. Introducere
Radioamatorii sunt interesati s? transfere un maxim de putere de la
emit?tor spre anten?. Scopul acestui articol este de a g?si conditiile în care
se produce transferul maxim de putere.
În general un emit?tor poate fi considerat un generator de putere cu
tensiune alternativ?, iar antena poate fi privit? ca un consumaor de energie
electric?.
Orice generator electric sau consumator de energie electric? are
rezistente, inductante si capacit?ti interne. Uneori aceste elemente de circuit
nu sunt dorite, situatie în care le numim "parazite", dar ele exist?. Este de
dorit, de exemplu, ca rezistenta ohmic? a înf?sur?rilor unui generator electric
de tensiune alternativ? s? fie cât mai mic?, pentru ca puterea disipat? pe
aceast? rezistent? s? fie, deasemenea, cât mai mic?. La un amplificator de
putere de RF cu tuburi este de dorit ca valoarea capacit?tii dintre anod si
gril? s? fie cât mai mic? pentru a evita autooscilatiile. Exemplele pot
continua.
Modul în care sunt interconectate aceste elemente interne de circuit
este practic necunoscut. Dar orice form? ar avea un astfel de circuit el va fi
totdeauna echivalent cu un circuit R, L, C serie. Este unanim acceptat ca
analiza diverselor circuite s? se fac? luând în considerare schema echivalent?
serie.
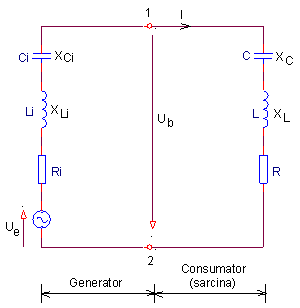
De aceea, în figura 1 este prezentat? schema echivalent? a unui
consumator conectat la un generator de tensiune alternativ?.
Fig. 1 Schema echivalent? a unui consumator conectat la un generator de
tensiune alternativ?
În tabelul 1 sunt prezentate simbolurile si ecuatiile de definitie ale
m?rimilor care intervin în circuitul din figura 1.
Tabelul 1
|
Nr.
Crt.
|
Simbolul
m?rimii si
ecuatia de definitie
|
Denumirea m?rimii
|
Unitatea de
m?sur?
|
|
1
|
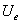
|
Valoarea efectiv?
a tensiunii electromotoare a generatorului
|
V
|
|
2
|
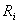
|
Rezistenta intern? a generatorului
|
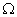
|
|
3
|
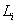
|
Inductanta intern?
a generatorului
|
H
|
|
4
|
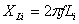
|
Reactanta
inductiv? intern? a generatorului
|
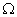
|
|
5
|
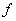
|
Frecventa
tensiunii generatorului
|
1/s = Hz
|
|
6
|
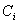
|
Capacitatea
intern? a generatorului
|
F
|
|
7
|
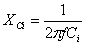
|
Reactanta
capacitiv? intern? a generatorului
|
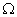
|
|
8
|
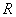
|
Rezistenta
consumatorului (a sarcinii)
|
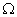
|
|
9
|
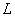
|
Inductanta
consumatorului
|
H
|
|
10
|
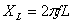
|
Reactanta
inductiv? a consumatorului
|
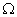
|
|
11
|
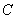
|
Capacitatea
consumatorului
|
F
|
|
12
|
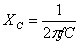
|
Reactanta
capacitiv? a consumatorului
|
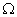
|
|
13
|
|
Valoarea efectiv?
a tensiunii la bornele generatorului
|
V
|
|
14
|
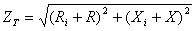
|
Impedanta total? a
circuitului
|
|
|
15
|
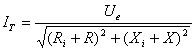
|
Valoarea efectiv?
a curentului prin circuit, în cazul în care reactanta total? a circuitului nu
este nul?,
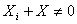
|
A
|
|
16
|
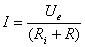
|
Valoarea efectiv?
a curentului prin circuit, în cazul în care reactanta total? a circuitului
este nul?,
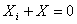
|
A
|
Într-un circuit serie, reactanta total? din circuit este egal? cu diferenta
dintre reactanta inductiv? si cea capacitiv?. Astfel, pentru generator si
pentru sarcin? se poate scrie:
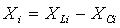
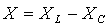 (1)
(1)
Dac? în relatiile (1) se va obtine 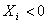 ,
înseamn? c? reactanta net? a generatorului este capacitiv?, iar în cazul
,
înseamn? c? reactanta net? a generatorului este capacitiv?, iar în cazul 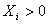 ,
reactanta net? a generatorului este inductiv?. Acelasi rationament se aplic? si
pentru recatanta net?
,
reactanta net? a generatorului este inductiv?. Acelasi rationament se aplic? si
pentru recatanta net?  a
consumatorului. Reactanta total? din circuitul prezentat în figura 1 este
a
consumatorului. Reactanta total? din circuitul prezentat în figura 1 este  ,
iar rezistenta total? din circuit este
,
iar rezistenta total? din circuit este 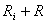 .
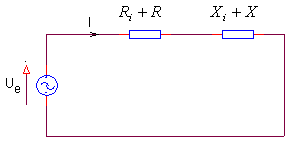
Cu aceste preciz?ri, circuitul din figura 1 este echivalent cu circuitul din
figura 2.
.
Cu aceste preciz?ri, circuitul din figura 1 este echivalent cu circuitul din
figura 2.
Fig. 2. Schema echivalent? a circuitului din Fig. 1
În general tensiunea generatorului este alternativ?. În acest caz,
limitarea curentului prin circuit se face de impedanta total? din circuit,
impedant? prezentat? la pozitia 14 în tabelul 1.
La pozitia 15 din tabelul 1 este prezentat? expresia valoarii efective a
curentului prin circuit, în conditiile neadapt?rii dintre generator si sarcin?,
adic? în cazul în care 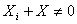 si
si
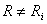 .
Am folosit acelasi indicele
.
Am folosit acelasi indicele 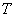 ca
si pentru impedanta total? a circuitului,
ca
si pentru impedanta total? a circuitului, 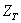 .
.
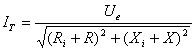 [A] (2)
[A] (2)
Puterea activ? este consumat? doar de rezistentele din circuit,
reactantele nu consum? putere, dar contribuie la limitarea curentului. Deci puterea
generatorului va fi disipat? doar pe rezistentele din circuit, adic? pe
rezistenta intern? a generatorului si pe rezistenta sarcinii.
Puterea consumat? numai de rezistenta sarcinii, notat? cu 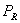 ,
în cazul în care
,
în cazul în care 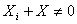 si
si
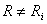 ,
(cu conditia
,
(cu conditia 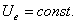 )
este dat? de relatia:
)
este dat? de relatia:
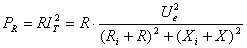 (3)
(3)
2. Reactantele din circuit sunt nule sau conjugate
Este posibil ca circuitul analzat s? nu aib? reactante, situatie în care
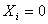 si
si 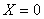 .
În acest caz în circuit vor r?mâne numai cele dou? rezistente între care se
doreste s? se fac? adaptarea.
.
În acest caz în circuit vor r?mâne numai cele dou? rezistente între care se
doreste s? se fac? adaptarea.
Deasemenea, dac? este îndeplinit? conditia:
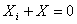 , sau
, sau 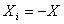 (4)
(4)
se spune c? reactanta net? a generatorului este conjugata
reactantei nete a consumatorului. Aceasta înseamn? c? dac? reactanta net? a
generatorului este inductiv?, atunci reactanta net? a consumatorului este
capacitiv?, si invers. În acest? situatie cele dou? reactante se vor anula reciproc
si în circuit vor r?mâne din nou numai cele dou? rezistente între care se
doreste s? se fac? adaptarea.
Din punct de vedere al analizei circuitului, cele dou? situatii în care
reactantele din circuit sunt nule sau conjugate sunt echivalente. De aceea în
continuare, în aceast articol, se va p?stra doar conditia 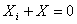 (sau
(sau 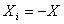 ).
).
În acest caz se vor analiza puterile disipate în circuit si randamentul
de transfer:
a) puterea disipat? pe rezistenta de sarcin?;
b) puterea disipat? pe rezistenta intern? a generatorului;
c) puterea total? disipat? în circuit;
d) randamentul de transfer al puterii active de la generator la sarcin?.
a) Puterea disipat? pe rezistenta de sarcin?
Pentru ca puterea disipat? pe rezistenta sarcinii s? fie maxim? trebuie
ca valoarea numitorului expresiei (3) s? fie minim?. Din punct de vedere al
reactantelor, acest lucru se întâmpl? atunci când 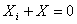 (
(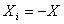 ). Considerând îndeplinit? acest? condie, puterea
). Considerând îndeplinit? acest? condie, puterea
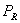 din
relatia (3), disipat? pe rezistenta sarcinii va avea o alt? expresie, de aceea
va fi notat? cu
din
relatia (3), disipat? pe rezistenta sarcinii va avea o alt? expresie, de aceea
va fi notat? cu 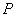 si
este dat? de relatia:
si
este dat? de relatia:
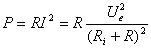 (5)
(5)
unde
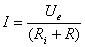 (6)
(6)
reprezint? valoarea efectiv? a curentului prin circuit în cazul în care 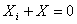 .
.
b) Puterea disipat? pe rezistenta intern? a
generatorului
Aceast? putere, notat? cu 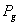 ,
este dat? de relatia:
,
este dat? de relatia:
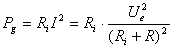 (7)
(7)
c) Puterea total? disipat? în circuit
Aceast? putere, notat? cu 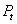 ,
este dat? de relatia:
,
este dat? de relatia:
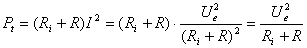 (8)
(8)
d) Randamentul de transfer al puterii al puterii
active de la generator la sarcin?
Randamentul transferului puterii active este definit ca raportul dintre
puterea disipat? pe rezistenta de sarcin? si puterea total? disipat? în
circuit:
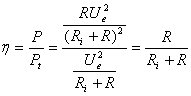 (9)
(9)
2. Conditiile de adaptere a sarcinii la generator
Se consider? în continuare satisf?cut? conditia 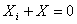 .
.
Prelucrând expresia (5) se obtine:
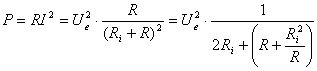 (10)
(10)
Primul termen al numitorului expresiei (10) este 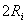 , care este constant, în sensul c?
generatorul este dat si nu-si poate modifica rezistenta intern?. Rezult? c?
numitorul este minim numai dac? al doilea termen al numitorului,
, care este constant, în sensul c?
generatorul este dat si nu-si poate modifica rezistenta intern?. Rezult? c?
numitorul este minim numai dac? al doilea termen al numitorului, 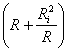 , este minim. Cum produsul dintre
, este minim. Cum produsul dintre 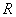 si
si 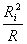 este constant (
este constant (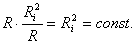 ), suma acestor termeni este minim? numai atunci
când termenii sunt egali, adic? atunci când:
), suma acestor termeni este minim? numai atunci
când termenii sunt egali, adic? atunci când: 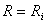 .
.
Rezult? c? cele dou? conditii ale transferului maxim
de putere activ? de la generator la sarcin? sunt:
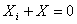 si
si
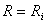 (11)
(11)
Conditiile g?site pentru adaptare se exprim? în cuvinte astfel:
Pentru ca o sarcin? s? absoarb? maximum de putere activ? de la un generator
trebuie ca rezistenta sarcinii s? fie egal? cu rezistenta intern? a
generatorului, iar reactanta sarcinii s? fie egal? si opus? cu reactanta
intern? a generatorului; dac? reactanta intern? a generatorului este inductiv?,
atunci reactanta sarcinii trebuie s? fie capacitiv? si invers, dar ambele s?
aib? aceeasi valoare absolut?. Se spune c? receptorul este adaptat cu
generatorul din punct de vedere al puterii maxime.
Si în acest caz se vor analiza puterile din circuit si randamentul de
transfer:
a) puterea maxim? ce poate fi transferat? sarcinii la conditiile de
adaptare;
b) puterea total? disipat? în circuit la conditiile de adaptare;
c)
randamentul corespunz?tor transferului maxim de putere.
a) Puterea maxim? ce poate fi transferat? sarcinii la
conditiile de adaptere
Dac? în relatia (5) se pune si conditia 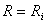 se obtine valoarea puterii maxime,
se obtine valoarea puterii maxime,
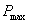 , ce poate fi transferat? de la generator la
receptor, la conditiile de adaptare:
, ce poate fi transferat? de la generator la
receptor, la conditiile de adaptare:
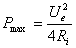 (12)
(12)
b) Puterea total? disipat? în circuit la conditiile
de adaptare
Dac? sunt îndeplinite simultan conditiile de adaptare, 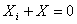 si
si 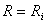 , atunci puterea total? disipat? în circuit,
notat? cu
, atunci puterea total? disipat? în circuit,
notat? cu 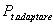 ,
se obtine din relatia (8) în care se pune suplimentar conditia
,
se obtine din relatia (8) în care se pune suplimentar conditia 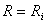 . Rezult?:
. Rezult?:
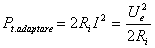 (13)
(13)
Interpretarea expresiei (13) este urm?toarea: în cazul adapt?rii,
jum?t?te din puterea generatorului se consum? pe propria rezistent? intern? si
cealalt? jum?tate pe rezistenta de sarcin?.
c) Randamentul
corespunz?tor transferului maxim de putere
Randamentul
corespunz?tor transferului maxim de putere este dat de relatia:
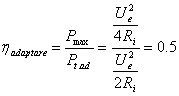 (14)
(14)
3. Reprezent?ri grafice
În cazul în care este îndeplinit? conditia 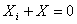 , este util de reprezentat grafic, în functie
de rezistenta de sarcin?
, este util de reprezentat grafic, în functie
de rezistenta de sarcin? 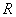 , urm?torii parametri:
, urm?torii parametri:
- puterea total? disipat? în circuit 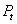 ,
relatia (8);
,
relatia (8);
- puterea disipat? pe rezistenta intern? a generatorului 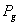 ,
relatia (7);
,
relatia (7);
- puterea disipat? de rezistenta de sarcin? 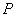 ,
relatia (5);
,
relatia (5);
- randamentul transferului puterii active de la generator la sarcin?,
relatia (9).
În fiecare dintre relatile (5), (7) si (8) apare termenul 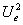 ,
care nu este cunoscut. Pentru ca totusi s? se poat? reprezenta grafic puterile
mentionate mai sus, acestea vor fi raportate la puterea maxim? ce poate fi
transmis? sarcinii,
,
care nu este cunoscut. Pentru ca totusi s? se poat? reprezenta grafic puterile
mentionate mai sus, acestea vor fi raportate la puterea maxim? ce poate fi
transmis? sarcinii,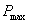 ,
dat? de relatia (11). În aceste fel se obtin urm?toarele puteri raportate:
,
dat? de relatia (11). În aceste fel se obtin urm?toarele puteri raportate:
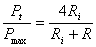 ;
; 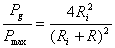 ;
; 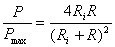 (15)
(15)
În relatiile (15) de mai sus, variabila este rezistenta sarcinii  . O simpl? reprezentare a puterilor raportate
mentionate, în functie de valoarea în ohmi a rezistenei sarcinii nu ne spune
nimic. Va trebui s? m?sur?m rezistenta sarcinii în multiplii ai rezistentei
interne
. O simpl? reprezentare a puterilor raportate
mentionate, în functie de valoarea în ohmi a rezistenei sarcinii nu ne spune
nimic. Va trebui s? m?sur?m rezistenta sarcinii în multiplii ai rezistentei
interne  . De aceea, în abscisa graficelor trasate va
fi reprezentat? rezistenta sarcinii
. De aceea, în abscisa graficelor trasate va
fi reprezentat? rezistenta sarcinii 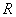 pân? la valoarea de
pân? la valoarea de 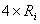 .
.
Înainte de a reprezenta grafic puterile raportate mentionate, este util
s? se întocmeasc? tabelul 2.
Tabelul 2
|
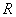
|
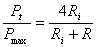
|
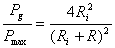
|
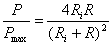
|
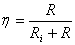
|
|
0
|
4
|
4
|
0
|
0
|
|
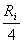
|
3.200
|
2.560
|
0.640
|
0.200
|
|
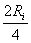
|
2.666
|
1.777
|
0.888
|
0.333
|
|
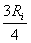
|
2.285
|
1.306
|
0.979
|
0.428
|
|
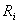
|
2
|
1
|
1
|
0.5
|
|
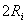
|
1.333
|
0.444
|
0.888
|
0.666
|
|
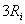
|
1
|
0.250
|
0.750
|
0.750
|
|
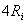
|
0.800
|
0.16
|
0.640
|
0.800
|
În tabelul 2 sunt calculate puterile raportate 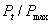 ,
,
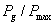 si
si
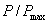 în
functie de rezistenta de sarcin?
în
functie de rezistenta de sarcin? 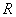 ,
care este exprimat? în submultiplii si multiplii ai rezistentei interne
,
care este exprimat? în submultiplii si multiplii ai rezistentei interne 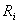 a
generatorului. Valorile din tabelul 2 se reg?sesc si în graficele din figura 3.
a
generatorului. Valorile din tabelul 2 se reg?sesc si în graficele din figura 3.
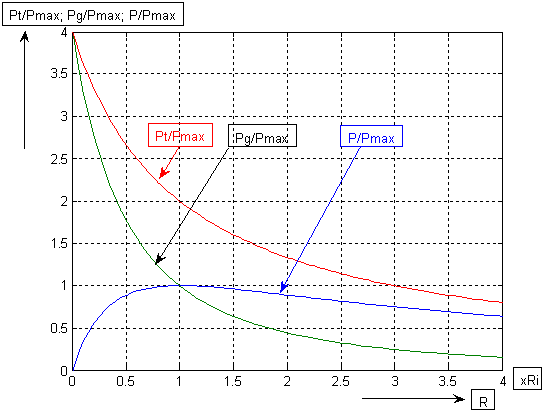
În figura 3 sunt reprezentate graficele puterilor raportate 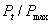 ,
,
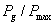 si
si
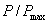 .
.
Fig. 3. Curbele puterilor raportate 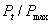 ,
,
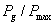 si
si
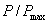 în
functie de rezistenta de sarcin?
în
functie de rezistenta de sarcin? 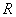 .
.
Din figura 3 se vede c? pentru 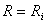 se
obtine
se
obtine 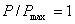 ,
adic?
,
adic? 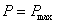 .
Aceast? relatie exprim? rezultatul deja cunoscut si anume c? puterea maxim?
transferat? sarcinii are loc atunci când
.
Aceast? relatie exprim? rezultatul deja cunoscut si anume c? puterea maxim?
transferat? sarcinii are loc atunci când 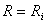 si
si
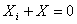 , adic? la adaptarea sarcinii la generator.
, adic? la adaptarea sarcinii la generator.
Tot pentru 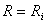 ,
din figura 3 se vede c?
,
din figura 3 se vede c? 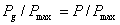 ,
adic?
,
adic? 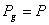 si
si
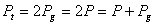 .
Acest rezultat se exprim? în cuvinte astfel: în cazul în care sunt îndeplinite
conditiile de adaptare,
.
Acest rezultat se exprim? în cuvinte astfel: în cazul în care sunt îndeplinite
conditiile de adaptare, 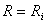 si
si
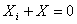 , jum?tate din puterea disponibil? în circuit
se disip? pe rezistenta sarcinii si jum?tate pe rezistenta intern? a
generatorului.
, jum?tate din puterea disponibil? în circuit
se disip? pe rezistenta sarcinii si jum?tate pe rezistenta intern? a
generatorului.
Deasemenea, tot din figura 3 se vede usor c? pentru 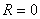 (rezistenta
sarcinii este nul?) puterea va fi disipat? doar pe rezistenta intern? a
generatorului si va fi de 4 ori mai mare decât puterea maxim?
(rezistenta
sarcinii este nul?) puterea va fi disipat? doar pe rezistenta intern? a
generatorului si va fi de 4 ori mai mare decât puterea maxim? 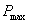 ce
poate fi transferat? sarcinii.
ce
poate fi transferat? sarcinii.
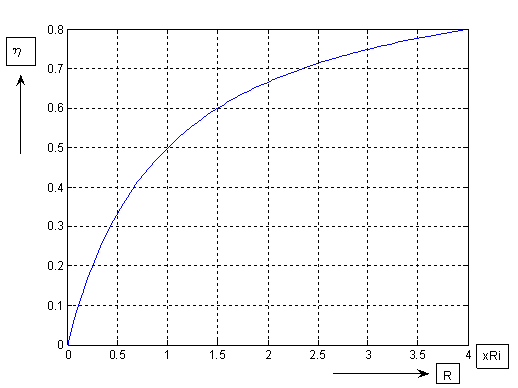
În figura 4 este reprezentat graficul randamentului transferului puterii
active de la generator la sarcin?.
Fig. 4. Curba randamentului transferului puterii active de la generator
la sarcin?, trasat? cu conditia ca reactanta total? din circuit s? fie nul?, 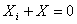 .
.
Se observ? c? pentru 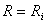 randamentul
de transfer este de numai 50%, ceea ce înseamn? c? 50% din putere se transmite
si se disip? pe sarcin? si 50% din putere se disip? pe rezistenta intern? a
generatorului.
randamentul
de transfer este de numai 50%, ceea ce înseamn? c? 50% din putere se transmite
si se disip? pe sarcin? si 50% din putere se disip? pe rezistenta intern? a
generatorului.
4. Concluzii
Din datele tabelului 2 si din graficele prezentate în figura 3 se
observ? c? pe m?sur? ce rezistenta de sarcin? 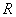 creste
si devine mai mare decât rezistenta intern?
creste
si devine mai mare decât rezistenta intern? 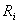 ,
puterea furnizat? sarcinii scade usor. Acest lucru se petrece pentru c? pe
m?sur? ce curentul absorbit de la generator scade, tensiunea de iesire creste;
rezult? c? sistemul posed? proprietatea de autoreglare atunci când este usor
înc?rcat. Atunci când rezistenta de sarcina devine de dou? ori mai mare decât
rezistenta intern? a generatorului, puterea livrat? sarcinii înc? este 89% din
puterea maxim? ce poate fi transmis?, ceea ce reprezint? o sc?dere de numai
0.51 dB.
,
puterea furnizat? sarcinii scade usor. Acest lucru se petrece pentru c? pe
m?sur? ce curentul absorbit de la generator scade, tensiunea de iesire creste;
rezult? c? sistemul posed? proprietatea de autoreglare atunci când este usor
înc?rcat. Atunci când rezistenta de sarcina devine de dou? ori mai mare decât
rezistenta intern? a generatorului, puterea livrat? sarcinii înc? este 89% din
puterea maxim? ce poate fi transmis?, ceea ce reprezint? o sc?dere de numai
0.51 dB.
Avantajul major al unei sarcini mici se vede din curba randamentului
prezentat? în figura 4. La conditiile de adaptere (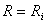 si
si 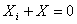 ) randamentul este de numai de numai 50%, dar
acesta creste la 67% (2/3) atunci când
) randamentul este de numai de numai 50%, dar
acesta creste la 67% (2/3) atunci când 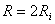 si
atinge 80% (4/5) când
si
atinge 80% (4/5) când 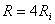 .
Aceasta înseamn? c? în cazul în care reactantele din circuit sunt conjugate (
.
Aceasta înseamn? c? în cazul în care reactantele din circuit sunt conjugate (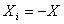 ) si când sarcina generatorului este mic?,
puterea disipat? pe rezistenta interna a generatorului este deasemenea mic?
(trebuie observat c? o rezistent? de sarcin? mare înseamn? sarcin? mic? si
invers).
) si când sarcina generatorului este mic?,
puterea disipat? pe rezistenta interna a generatorului este deasemenea mic?
(trebuie observat c? o rezistent? de sarcin? mare înseamn? sarcin? mic? si
invers).
În domeniul radio generatorul este emit?torul. Dac? emit?torul este
proiectat pentru o sarcin? mic?, atunci consumul s?u de la baterie sau de la
retea va fi mic, iar radiatoarele de r?cire ale tranzistorilor din etajul final
vor fi, deasemenea, de dimensiuni mici, în comparatie cu un emit?tor proiectat
pentru o sarcin? conjugat?. În consecint? cifra care reprezint? "impedanta
de iesire" a emit?torului radio (cea mai frecvent? fiind 50  )
nu reprezint? nimic alteceva decât rezistenta de sarcin? preferat? a
emit?torului sau altfel spus rezistenta de sarcin? proiectat?.
)
nu reprezint? nimic alteceva decât rezistenta de sarcin? preferat? a
emit?torului sau altfel spus rezistenta de sarcin? proiectat?.
Rezistenta de sarcin? preferat? a unui amplificator de band? larg? cu
tranzistor este de obicei mai mare decât impedanta de iesire, si încercarea de
a-i oferi unui astfel de amplificator o adaptare conjugat? va conduce la o
disipare intern? excesiv?, supraînc?lzind sau chiar distrugând amplificatorul.
Din fericire, majoritatea amplificatoarelor moderne sunt prev?zute cu
circuite de protectie care previn supraînc?lzirea. Aceste circuite îi ofer?
emit?torului o astfel de caracteristic? de sarcin? care fac s? par? c?
rezistenta emit?torului ar fi mai mare decât este în realitate. Caracteristica
de sarcin? va fi diferi de curba puterii transferat? sarcinii (curba 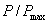 din
figura 3), pentru c? ea este obtinut? cu ajutorul unor elemente neliniare de
circuit (detectoare de nivel, etc.) si în acest fel rezistenta de sarcin?, care
corespunde regiunii centrale a ferestrei de operare permise, este cunoscut? ca
impedant? de iesire fals? ("pseudo output-impedance" sau "pseudo-source
impedance").
din
figura 3), pentru c? ea este obtinut? cu ajutorul unor elemente neliniare de
circuit (detectoare de nivel, etc.) si în acest fel rezistenta de sarcin?, care
corespunde regiunii centrale a ferestrei de operare permise, este cunoscut? ca
impedant? de iesire fals? ("pseudo output-impedance" sau "pseudo-source
impedance").
În figura 5 este prezentat cum ar putea ar?ta curba transferului de
putere cu fereastra de operare centrat? pe o rezistent? de sarcin? de dou? ori
mai mare decât rezistenta intern? a generatorului (functia de transfer neprotejat?
este ar?tat? de linia mai subtire, cea de culoare albastr?).
Este de observat c? circuitele de protectie functioneaz? si în cazul în
care rezistenta de sarcin? este mai mare decât valoarea preferat?. Acest lucru
nu este neap?rat necesar pentru protejarea amplificatoarelor de putere cu
tranzistori în push-pull; dar aceste circuite ajut? ca filtrul de suprimare a
armonicelor amplasat dup? amplificator s? functioneze corect. Impedanta de
sarcin? este în mod traditional detectat? utilizând un circuit punte care se
echilibreaz? pentru o valoare particular? a rezistentei. Acest circuit punte
este adesea denumit reflectometru sau punte SWR, dar în realitate este o punte
de impedante.
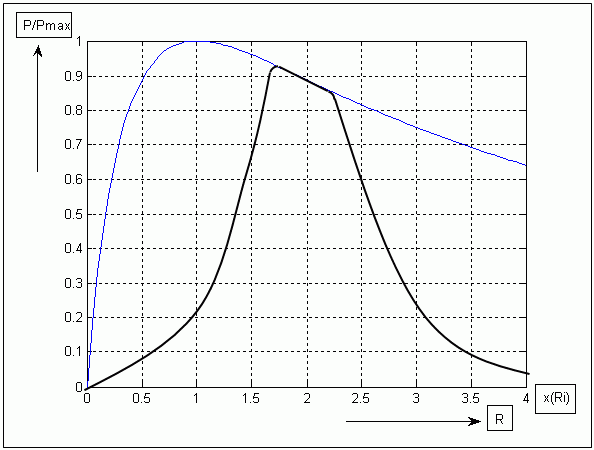
Fig. 5. Caracteristica de sarcin? a emit?toarelor moderne, centrat? pe o
rezistent? de sarcin? de dou? ori mai mare decât rezistenta intern? a
generatorului
Dac? circuitele de protectie sunt corect proiectate si reglate, pseudo
impedanta de iesire trebuie s? fie aceeasi cu rezistenta de sarcin? preferat?.
În cazul în care se determin? efectul impedantei sursei asupra factorului Q al
sistemuli de anten? si a filtrelor trece band? se va lua în considerare
impedanta real? de iesire si nu se va tine cont de rezistenta de sarcin?
preferat?. Din nefericire aceast? valoare este aproape imposibil de obtinut din
datele produc?torilor de emit?toare, dar poate fi m?surat? cu ajutorul a dou?
rezistente de sarcin? artificiale de valori diferite.
O discutie interesant? despre efectul impedantei de sarcin? asupra
eficientei amplificatorului de putere si asupra conditiilor care provoac?
distrugerea tranzistorilor este tratat? în "How Big is a Bad SWR?"
de Bob Pearson, G4FHU, Rad Com (RSGB Journal), March 1993, p64-65, April
1993, p62-63.
O descriere sumar? a acestui articol este f?cut?, deasemenea, tot de Dr.
David Knight:
"Cel mai mare pericol pentru amplificatoarele cu tranzistori în
push-pull se ascunde în rezistenta de sarcin?. Pentru o valoare dat? a
SWR-ului, efectul unei rezistente de sarcin? cu valoare sc?zut? este mai
periculos decât efectul reactantei. Criteriul de obtinere al adaptarii
utilizând un SWR-metru este destul de slab pentru c?, el nu indic? dac? m?rimea
impedantei de sarcin? este prea mare, situatie care nu creaz? probleme, sau
prea mic?, situatie în care pot apare deranjamente. În absenta unor informatii
referitoare la sarcin? cel mai bine este s? se opereze cu cel mai mic SWR
posibil."