PROPAGAREA LA DISTANŢĂ de Gheorghe Oproescu-Tavi

Articole > Echipamente si constructii radio

Comentati acest articol Tipariti

PROPAGAREA LA DISTANŢĂ

Gheorghe Oproescu-Tavi YO4BKM

Am văzut în apariţiile din ultimul timp un interes crescut pentru aspectele tehnice ale propagării la distanţă, dar şi noutăţi, toate acestea provocând comentarii interesante. Apreciind în mod deosebit lucrările amicului Florin YO8CRZ, care ne-a pus la dispoziţie materiale inedite şi de prima mână, consider că ce urmează nu este decât o colegială completare în sensul adăugării unor faţete noi. Sau un alt mod de prezentare, cu alte mijloace, la care încerc să contrubui şi eu cu câte ceva. Iau în considerare şi faptul că de multe ori un fenomen prea bine cunoscut de autor poate fi prezentat cu mai puţină claritate din cauza unui instinct derutant: fiind furat de prezentare, autorul uită adesea cât de greu a ajuns la cunoaşterea pe care o prezintă şi neglijează, fără să vrea, detalii importante, nici eu nu am fost şi nici nu sunt scutit de acest lucru. Publicaţiile lui YO8CRZ şi mesajele schimbate între noi au dus la cristalizarea anumitor idei pe care le prezint mai jos.

De peste 60 de ani atmosfera înaltă este cercetată cu baloane, rachete meteo, sateliţi specializaţi, în cadrul unor programe de interes militar, comercial sau ştiinţific. Se monitorizează continuu activitatea Soarelui, centre de cercetare dezvoltă modele ale instrumentaţiei virtuale cu pretenţii de a fi tot mai exacte în privinţa comportării atmosferei la orice moment. În aceste condiţii este de aşteptat să fie cât mai facilă şi mai exactă orice predicţie prin simulare pe calculator a condiţiilor de propagare pe orice direcţie. În măsura în care am elaborat şi eu destule aplicaţii de instrumentaţie virtuală, cele mai multe în dinamica structurilor, înţeleg destul de bine care sunt complicaţiile la elaborarea unui astfel de soft dar, la fel de bine, înţeleg şi că softurile chiar făcute de firme puternice au limitări produse nu din nepricepere sau din dorinţa de a înşela, ci din prea puţine resurse avute la dispoziţie.

1. Spaţiul undelor radio şi orientarea antenei.

Text Box:
Figura 1. Distanţele pe plan (roşu) şi pe sferă (albastru). Harta de la [ 4 ] Comunicaţiile pe distanţe mari la nivel terestru se produc într-un spaţiu neeuclidian, în care nu mai este valabilă geometria clasică. Pe o sferă drumul cel mai scurt dintre două puncte nu mai este o linie dreaptă ca pe un plan, ci o geodezică, adică o curbă care rezultă din intersecţia sferei cu un plan care trece prin centru. Într-un caz ideal (Pământul este sferic iar straturile ionizate sunt concentrice cu suprafaţa Pământului) undele de câmp electromagnetic se propagă între două puncte urmărind liniile geodezice. Dacă studiem pe un planiglob (sfera terestră transpusă în plan după anumite reguli de proiecţie) distanţele şi traseele între puncte depărtate, apar erori de orientare, figura 1, produse de deformarea suprafeţei sferice cu tot ce are pe ea când este transpusă într-un plan. Pe figură am considerat punctul A ca fiind în Bucureşti, punctul B₁ în Sidney iar punctul B₂ în Tokyo. Segmentele de dreaptă trasate cu roşu ar arăta distanţele şi direcţiile dacă lumea ar fi plană, aşa cum apare pe planiglob. În realitate distanţele cele mai scurte pe suprafaţa terestră sferică, geodezicele de care am vorbit, apar pe planiglob sub forma segmentelor de curbe colorate în albastru care, în mod ciudat, la prima vedere par că sunt mai lungi decât liniile roşii. Numai că liniile roşii arată distanţe pe o hartă puternic deformată datorită trecerii de la sferă la plan. De aici apare o primă eroare, eroarea de orientare a antenei sau a lobilor săi în plan orizontal. Se vede că în punctul A din figura 1 între linia roşie şi tangenta la linia albastră se formează un unghi uşor sesizabil care, aşezat pe o diagramă de radiaţie în plan orizontal al unei antene, va arăta modificări ale câştigului antenei, figura 2, modificări cu atât mai mari cu cât antena este mai directivă.

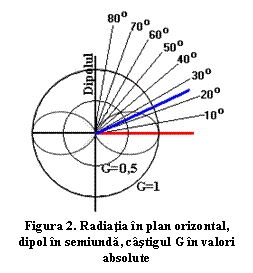
Text Box:
Figura 2. Radiaţia în plan orizontal, dipol în semiundă, câştigul G în valori absolute Orientarea lobului de radiaţie al antenei spre un loc ales pe Pământ folosindu-ne de o hartă plană nu se poate face exact decât cu calcule de corecţie faţă de direcţia rectilinie arătată de segmentul roşu din figura 1, corecţii funcţie de tipul proiecţiei cu care s-a realizat harta (cilindrică, azimutală, conică, Mercator, Gauss – Krüger, fiecare din acestea având multiple variante). Sunt şi programe de calculator care oferă pentru orice locaţie azimutul corect pe care se află orice partener de pe suprafaţa Pământului, acestea folosesc trigonometria sferică (într-un spaţiu neeuclidian) care, din nu ştiu ce motive, nu se studiază nici măcar la nivel universitar decât cu excepţia specializărilor din domeniul matematicii sau la navigaţie aeriană ori maritimă. Ciudată această lipsă dacă ne gândim că, de când se navighează pe un Pământ sferic (cel puţin de câteva secole), navigatorii au "la degetul mic" această trigonometrie.

În lipsa unui program de calculator ne putem folosi de un simplu glob terestru. Se poate trasa pe el un cerc cu raza de cca 5 cm cu centrul în localitatea unde ne aflăm şi, unde cercul se intersectează cu meridianul locului care duce spre Nord, acolo se află originea azimutului geografic. Se împarte cercul din 30 în 30 de grade (dacă se poate din 10 în 10 grade ar fi şi mai bine), având ca punct de pornire originea azimutului geografic. Direcţia spre Polul Nord magnetic, arătat de busolă la nivelul Bucureştiului, este decalată cu 5⁰06' spre vest faţă de Polul Nord geografic (declinaţia magnetică). Azimutul geografic al direcţei care ne interesează se află întinzând un fir elastic între centrul cercului trasat pe globul pământesc şi punctul care ne interesează (cel mai bine este să fixăm aceste poziţii cu două bolduri, iar firul elastic se aşează sigur pe geodezica dintre bolduri dacă, după ce este întins, se ciupeşte de câteva ori, ocupând astfel poziţia cea mai puţin tensionată conform cunoscutului principiu al minimei acţiuni al lui Maupertuis) şi citind valoarea azimutului geografic pe cercul gradat ca mai sus. Dacă orientarea antenei se face folosind busola, deci după azimutul magnetic, la valoarea citită se mai adaugă declinaţia magnetică de 5⁰06'. La acest azimut se va poziţiona antena rotativă sau vom cunoaşte cum este poziţionată această direcţie faţă de lobii de radiaţie în plan orizontal ai antenei fixe.

Şi iată care sunt rezultatele în cazul traseului scurt Bucureşti-Tokyo: dacă se măsoară pe glob, rezultă un azimut de cca 53⁰ faţă de nordul geografic (în figura 3 firul elastic care pleacă din punctul A se ridică spre Nord în raport cu cercurile paralele care dau direcţia Est) sau cca 58⁰ faţă de nordul magnetic. Dacă se măsoară pe planiglobul radioamatorilor, rezultă un azimut de cca 95⁰ faţă de acelaşi nord geografic (în figura 1 direcţia rectilinie trasată cu roşu coboară spre sud în raport cu direcţia Est). O diferenţă enormă!

Text Box:
Figura 3. Drecţia A-B2 pe glob Ce am arătat până acum se referă la un caz idealizat, un Pământ sferic şi neted, un strat reflectător în ionosferă tot sferic şi concentric cu Pământul.

2. Reflexiile simple şi reflexiile multiple într-o prezentare simplificată.

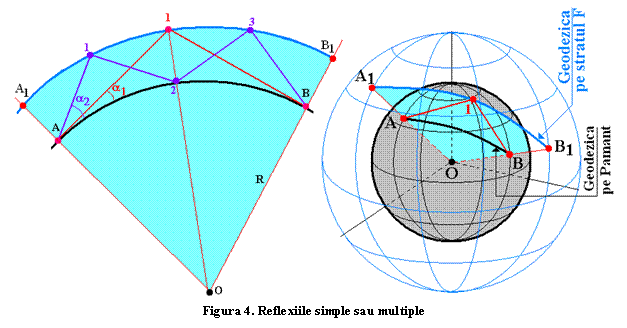Text Box:
Figura 4. Reflexiile simple sau multiple Se cunosc poziţiile pe glob ale celor două staţii radio între care se doreşte a se stabili o comunicare, notate cu A şi B. În figura 4 arcul de cerc AB este geodezica de pe Pământ care trece prin punctele A şi B, O este centrul Pământului, A₁ şi B₁ sunt geodezicele de pe stratul F, toate cuprinse în acelaşi plan O-A-A₁-1-B₁-B-O. Din păcate sunt singurele lucruri cunoscute cu precizie. De aici încolo urmează presupunerile, ipotezele şi aproximările. Pentru început presupunem că reflexia pe ionosferă se produce la înălţimea H de suprafaţa Pământului, stratul ionizat F este tot sferic şi concentric cu Pământul, suprafaţa Pământului este sferică cu raza R=6380 km, netedă, fără forme de relief.

Undele emise din A ajung în B fie pe traseul desenat cu roşu, printr-o singură reflexie în punctul 1 plecând sub unghiul a₁în raport cu orizontala loculuilocului, fie pe traseul desenat cu albastru prin trei reflexii în punctele 1, 2 şi 3, plecând sub unghiul a₂ în raport cu acceaşi orizontală, unghiuri care se pot afla din simple calcule trigonomentrice. Din motive de simetrie aceste unghiuri au aceeaşi valoare pentru fiecare din cele două locuri A şi B. Pentru două locuri A şi B concrete direcţiile a pe care pleacă sau sosesc undele radio nu pot avea orice valoare, deoarece numărul de reflexii trebuie să fie obligatoriu impar, trebuie să înceapă şi să se termine în punctele A şi B iar traseul undelor este obligatoriu simetric în raport cu bisectoarea unghiului AOB. După cum se arată detaliat în [1] traseul albastru A-1-2-3-B fiind mai lung, va avea pierderi prin reflexii şi absorbţii mai mari decât traseul roşu A-1-B.

Text Box: Tabelul 1. Distanţa maximă la o reflexie
H (km) 100 200 300 400 500
d (km) 2240 3160 3840 4400 4900 Pentru o înălţime H cunoscută, o singură reflexie nu poate asigura comunicaţii între puncte aflate la orice distanţă. În tabelul 1 sunt date distanţele "d" calculate pe geodezică (lungimea arcului de cerc) pentru unghiuri de plecare a de 0⁰, pentru care teoretic se obţin cele mai mari distanţe dintr-o singură reflexie. Înălţimea H la care poate exista în realitate stratul F nu depăşeşte valoarea de 500 km. Comunicaţia realizată ca în figura 4 corespunde unui traseu scurt (short pass) dintre punctele A şi B, dar se poate realiza şi pe traseul opus (long pass) printr-un număr mult mai mare de reflexii. Comparând unghiul de radiaţie maximă al unei antene reale în plan vertical cu direcţiile posibile pentru care se realizează comunicarea între cele două staţii, practica arată că de multe ori se efectuează mai uşor legături pe trasee mai lungi (sau pe trasee cu mai multe reflexii) in detrimentul traseului scurt sau cu mai puţine reflexii.

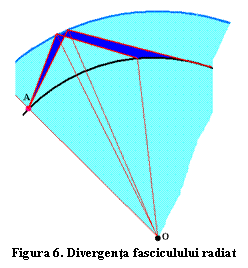
Text Box:
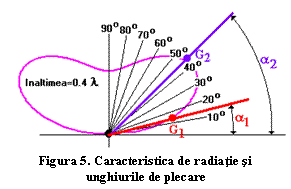Figura 6. Divergenţa fasciculului radiat Text Box:
Figura 5. Caracteristica de radiaţie şi unghiurile de plecare Figura 5 arată că pentru o antenă dipol orizontal aflată la o înălţime de 0,4 lungimi de undă faţă de sol direcţia de plecare sub unghiul a₂, pentru care se produc mai multe reflexii, deci şi pierderi mai mari prin reflexii şi absorbţii, beneficiază de un câştig mai mare al antenei, G₂, decât direcţia de plecare dată de a₁ cu G₁. Important este de ştiut dacă câştigul G₂ al antenei întrece sau nu pierderile produse de traseul cu mai puţine reflexii. Dar, cu totul alta ar fi fost situaţia dacă antena ar fi avut lobul cu câştig maxim chiar pe direcţia a₁, cum se întâmplă la antenele verticale de tip Marconi sau la antenele Yagi-Uda. Mai apare o situaţie: ce se întâmplă dacă niciuna din direcţiile de plecare a nu "pică" pe direcţia de radiaţie maximă a antenei cu câştig maxim, ci pe o direcţie unde câştigul este mai mic? Acoperirea pierderilor provocate de reflexii şi de câştigul insuficient se face prin mărirea puterii la emisie.

3. Cum arată realitatea.

O primă abatere a realităţii faţă de modelele de mai sus o reprezintă divergenţa fasciculului radiat de antenă, figura 6. În limitele unei scăderi nesemnificative a câştigului antenei, radiaţia în plan vertical se poate considera divergentă. Dacă divergenţa ar fi de cca 10⁰, la un parcurs de cca 5000 de km fasciculul ar crea o "pată" cu un diametru de cca 800 de km. Această abatere ar putea fi una favorabilă prin mărirea ariei acoperite la distanţă, dar produce şi o micşorare a densităţii de energie din fascicul.

O altă abatere este dată de suprafaţa Pământului care are atât denivelări produse de relief dar şi o formă nesferică, numită geoid.

Aceste denivelări ale suprafeţei terestre au drept consecinţă modificarea modului în care se produc reflexiile, complicând calcularea valorilor unghiurilor de plecare-sosire şi făcând ca aceste unghiuri sa nu mai fie egale la cei doi corespondenţi. În figura 7 este arătat un astfel de caz. 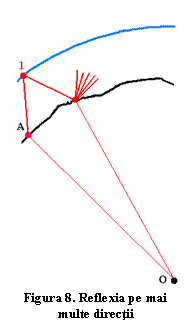Text Box:
Figura 8. Reflexia pe mai
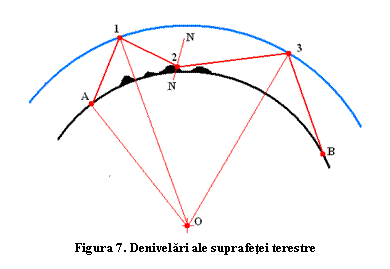multe direcţii Text Box:
Figura 7. Denivelări ale suprafeţei terestre În punctual de reflexie 2 există o abatere de la sfericitatea globului terestru, sunt suficiente câteva grade ca să producă devieri semnificative ale undei reflectate. Mai mult, relieful terestru poate fi astfel înclinat încât normala N-N la suprafaţa sa (figura 7) să nu mai aparţină planului geodezicei, ceea ce are ca efect schimbarea semnificativă a azimutului undei reflectate după reflexia survenită pe Pământ. În locurile cu relief foarte accidentat se pot produce reflexii pe direcţii multiple, în planul geodezicei dar şi în afara lui, figura 8, care au ca efect, pe de o parte, scăderea densităţii de energie pe fiecare din aceste direcţii, pe de altă parte creşterea divergenţei şi mai multe posibilităţi de a ajunge la diferiţi parteneri, dacă emiţătorul debitează suficientă putere.

Cartografierea tot mai precisă a suprafeţei terestre, fapt observabil şi pe un simplu navigator GPS care, cu abateri de ordinal metrilor, oferă coordonatele locului şi înălţimea sa faţă de nivelul mării, poate face posibil ca softurile de asistenţă a propagării să ia în calcul şi astfel de situaţii, formalismul matematic introdus suplimentar nu este atât de complicat precum cel folosit de algoritmii din softul unui navigator GPS.

Am prezentat aceste abateri relativ minore înaintea altora deoarece, oricât de complicată ar părea rezolvarea lor, ele sunt deterministe şi pot fi luate în considerare cu precizie. Iar furnizorul de software pentru asistenţă la propagare trebuie să precizeze dacă a fost luată în considerare forma reală a suprafeţei terestre, din această precizare ne putem da seama dacă softul poate fi aplicat corect pentru orice traseu de pe glob.

Text Box:
Figura 9. Ionosfera şi modelul ei [5] Cele mai mari şi imprevizibile abateri provin însă din evaluarea valorilor pentru stratul F precum poziţia, înălţimea H deasupra Pământului şi forma sa. Stratul nu apare în toată ionosfera, ionosfera nu este nici sferică şi nici concentrică cu Pământul (figura 9), există abateri faţă de modelul idealizat de mai sus şi toate acestea au ca efect, în primul rând, desimetrizarea traseului şi inegalitatea unghiurilor de plecare-sosire la cele două staţii chiar dacă suprafaţa terestră ar fi perfect sferică. Mai mult decât atât, în punctul de reflexie pe stratul F (de fapt o pseudoreflexie, în realitate este o refracţie continuă care se produce în grosimea acestui strat şi curbează continuu unda până o întoarce în mediul din care a venit) acest strat poate avea normala orientată pe o direcţie care nu mai aparţine planului geodezicei dintre punctele A şi B, pseudoreflexia face ca unda reflectată să părăsească acest plan iar undele vor suferi o altă schimbare de direcţie în privinţa azimutului. Pseudoreflexia pe stratul F (o voi numi totuşi în continuare, pentru simplificare, reflexie), se face în mod diferit pentru frecvenţe diferite şi unghiuri de plecare a de valori diferite, figura 10.

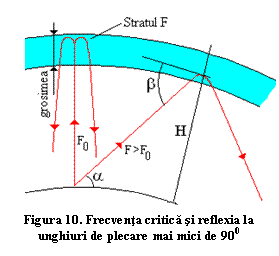Text Box:
Figura 10. Frecvenţa critică şi reflexia la unghiuri de plecare mai mici de 900 Valoarea maximă a frecvenţei la care unda, sub incidenţă normală în raport cu ionosfera, încă se mai întoarce înapoi în atmosferă (după alţii, de la această frecvenţă nu se mai întoarce, în realitate este un caz de limită) se numeşte frecvenţă critică, F₀. Valoarea acestei frecvenţe depinde de starea de ionizare a atmosferei înalte sub influenţa radiaţiei solare şi se calculează cu formula [5]:

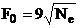[Hz] (1)

Text Box:
Figura 11. Valori extreme pentru [5] unde 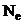este numărul de electroni liberi pe metru cub (densitatea de electroni liberi). Valorile extreme între care poate exista acest număr sunt arătate în figura 11. Dacă alegem o valoare medie 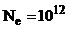la o înălţime de 300 km se obţine 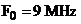. Micşorând unghiul de plecare de la 90⁰ la o valoare a reflexia se produce pentru frecvenţe mai mari decât frecvenţa critcă. Am impresia că aici au apărut nişte confuzii la determinările cantitative în sensul că s-a considerat unghiul de plecare faţă de orizontală, a, ca fiind acelaşi cu unghiul de incidenţă pe stratul F, b, figura 10. Cred că confuziile au fost generate considerând stratul F şi Pământul sfere ideale şi concentrice şi extinzând asupra lor regulile unghiurilor alterne interne, cuprinse între paralele, într-un anumit fel cele două sfere dau impresia că sunt paralele deoarece distanţa dintre ele este aceeaşi pe toată circumferinţa lor. În realitate, pentru un unghi de plecare a, raza Pămâmtului R şi o înălţime H a stratului ionizat F, unghiul de incidenţă b cu stratul F, măsurat faţă de tangenta la strat, figura 10, depinde de unghiul de plecare a după relaţia

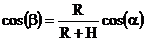(2)

Pe aceste considerente, frecvenţa F la care are loc reflexia undelor care pleacă sub unghiul 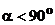, numită şi frecvenţă maximă utilizabilă (MUF [1]) se calculează cu

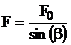(3)

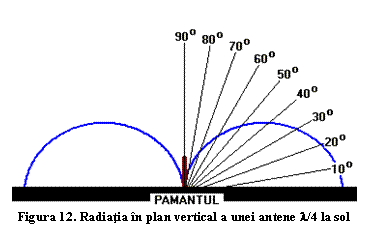Text Box:
Figura 12. Radiaţia în plan vertical a unei antene l/4 la sol care este, evident, mai mare decât frecvenţa critică F₀. Explicaţia stă în faptul că cu cât unghiul a este mai mic, deci şi unghiul b scade, traseul undei în grosimea stratului F devine mai lung iar refracţia care se produce continuu are loc să curbeze unda mai mult. În sursele care apar la bibliografie şi se referă la frecvenţa maximă utilizabilă [1], [5], se foloseşte în relaţia (3) unghiul a în loc de b, ceea ce conduce la o imposibilitate: pentru un unghi a=0 (ca la o antenă verticală pusă la Pământ, precum antena Marconi, figura 12) ar rezulta o frecvenţă maximă utilizabilă infinit de mare, adică folosind astfel de antene nicio undă radio, chiar de sute de MHz sau GHz, să nu mai părăsească atmosfera terestră, fenomen neîntâlnit în realitate.

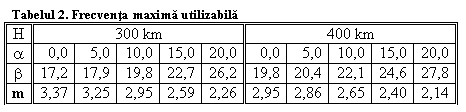Text Box: Tabelul 2. Frecvenţa maximă utilizabilă
H 300 km 400 km
a 0,0 5,0 10,0 15,0 20,0 0,0 5,0 10,0 15,0 20,0
b 17,2 17,9 19,8 22,7 26,2 19,8 20,4 22,1 24,6 27,8
m 3,37 3,25 2,95 2,59 2,26 2,95 2,86 2,65 2,40 2,14 În realitate, pentru un unghi a=0 şi o înălţime H=400 km rezultă b=19,78⁰ pentru care frecvenţa maximă utilizabilă este de 2,95 ori mai mare decât frecvenţa critică, nicidecum infinit de mare. În cazul unui unghi de plecare a=30⁰ s-ar obţine, pentru aceeaşi valoare a lui H, un unghi b=35,4⁰ iar frecvenţa maximă utilizabilă va fi de 1,72 ori mai mare decât frecvenţa critică. Dacă ar fi posibil ca unghiul b să devină egal cu zero, atunci sigur ar fi posibilă o frecvenţă maximă utilizabilă foarte mare, dar nu infinit de mare. Frecvenţa ar deveni infinit de mare pentru b=0 dacă stratul F ar avea o formă plană în loc de sferică, adică ar aparţine unui spaţiu euclidian. Iar această eroare are efecte destul de pronunţate la valori mici ale unghiului a, exact valorile recomandate pentru DX, a se vedea datele din tabelul 2, unde m este coeficientul de multiplicare a frecvenţei critice pentru a obţine frecvenţa maximă utilizabilă. Se mai vede ceva interesant: pentru straturi F joase, deşi între staţiile corespondente sunt necesare mai multe reflexii, frecvenţa maximă utilizabilă este mult mai mare decît pentru straturi F înalte. Valorile indicate de [1] pentru acest coeficient de multiplicare m ar fi corecte dacă respectivul unghi s-ar forma între unda incidentă şi tangenta la ionosferă, ori acest unghi nu poate fi oricât de mic din cauzele arătate. Faptul că frecvenţa maximă utilizabilă are uneori valori neaşteptat de mari şi duce la recepţionarea la mare distanţă în domeniul frecvenţelor înalte şi foarte înalte se explică prin ionizarea mult mai intensă decât normalul a stratului F la înălţimi joase, adică prin creşterea frecvenţei critice şi micşorarea unghiului b, deoarece această anomalie se manifestă în trafic obişnuit, fără să fie modificate caracteristicile antenelor, unghiul a rămânând neschimbat.

Relaţia (2) este corectă numai dacă am considera că undele radio se propagă rectiliniu până la stratul F. În realitate acestea suferă o refracţie prin toată atmosfera datorită modificării vitezei de propagare (permeabilitatea magnetică, permitivitatea dielectrică şi ionizarea se modifică cu înălţimea), propagarea lor fiind după o linie curbă în planul geodezicei, cel mai adesea cu concavitatea spre Pământ, ceea ce face ca unghiul b să rezulte mai mic decât valoarea calculată, lucru favorabil. Arăt că şi acest lucru este cunoscut în permanenţă, ştiu că navigatoarele GPS ţin cont de variaţia vitezei undei radio când trece prin diferite straturi ale atmosferei, această viteză fiind măsurată continuu de sateliţii de navigaţie.

Folosind relaţiile (1)---(3) precum şi figura 11 se poate estima la ce ne putem aştepta funcţie de activitatea Soarelui şi caracteristicile antenei din dotare. Asta cu condiţia ca, pentru direcţiile de radiaţie maximă ale antenei din dotare, să existe straturi F convenabil plasate. Dacă nu, va trebui să ne resemnăm cu ideea că putem atinge stratul F şi pe alt unghi de plecare, la care antena are un câştig considerabil mai redus şi este nevoie de putere pentru a compensa pierderile. Sau să facem precum vulpea care nu ajunge la struguri, dar o vulpe modernă poate înlocui strugurii cu alte delicatese. Din cele arătate mai sus se mai vede că un unghi optim de plecare nu trebuie să fie neapărat mic sau mare, ci trebuie să aibe exact valoarea rezultată din condiţia realizării unui număr impar şi cât mai mic de reflexii între staţiile corespondente.

Cunoaşterea la orice moment (în timp real) a unei hărţi a stratului F, cu frecvenţele critice şi înălţimea lui deasupra Pământului şi cuplarea softului cu care se cercetează propagarea la o bază de date mereu împrospătată cu cele mai noi ar putea reprezenta un ajutor de seamă pentru traficul radio. Folosirea în softurile de cercetare a propagării a unor modele probabilistice ale ionosferei [6] neconcentrică cu Pământul, create pe înregistrări prelucrate statistic pe un anumit interval de timp, reprezintă un alt ajutor valoros. Dar nu trebuie nici să se cadă în extrema idealizării lor. Exemplul arătat mai sus privind confuzia între unghiurile a şi b, care s-a extins cu viteza internetului, arată ce se poate întâmpla dacă nu se verifică informaţiile. Mai ales când acordăm încredere nelimitată surselor de informare. Cât priveşte modelele statistice ale ionosferei, în sensul în care am arătat mai sus, acestea pot ajuta mult mai mult dacă sunt corelate, dar şi acordate cu condiţiile existente oriunde pe suprafaţa şi în atmosfera Pământului şi care diferă de la un loc la altul. Dacă acelaşi model se aplică între staţii aflate la Londra şi Sidney sau între staţii aflate la Vladivostok şi Johannesburg, care ar putea folosi simultan acelaşi strat F, este uşor de înţeles că rezultatele vor trebui să fie diferite datorită existenţei altor forme de relief sub el dar şi a altor particularităţi precum aer umed, aer uscat, temperaturi şi presiuni barometrice diferite. Atunci când se elaborează un model pe calculator apoi un soft de lucru, punerea sa la punct se face după un şir de ajustări făcute de programator (precum probele la croitor), această fază se numeşte acordarea modelului prin comparare cu datele oferite de un anumit număr de experimente. Ştiu bine acest lucru din practica proprie şi, mai mult, am văzut cum firme cu mare forţă în instrumentaţie virtuală ajustează modelul furnizat, folosind experienţa empirică acumulată de client în domeniu, aceste aspecte fiind prevăzute în contractul de achiziţionare, să nu semene a furt de informaţii. În acest fel, cel care a produs modelul acumulează date şi experienţă de la clienţi pe banii plătiţi de clienţi dar care, la rândul lor, se dotează cu instrumente care le vin în ajutor cu maximă eficienţă, un parteneriat reciproc profitabil. În cazul nostru, dacă modelul folosit la cercetarea propagării la distanţă a fost acordat, de exemplu, pe traseul Londra-Sidney în urma mai multor teste practice, sigur nu va fi la fel de precis pe alte trasee care diferă în privinţa reliefului terestru sau a atmosferei şi pentru care nu a fost făcută acordarea prin măsurători practice. De aici se poate înţelege că pot exista modele din cele mai diferite ascunse în spatele unui soft mai mult sau mai puţin atrăgător sau, cel puţin, disponibil, cu care se fac chiar demonstraţii convingătoare dar care, de exemplu, este posibil să nu dea informaţii privind ipotezele cu care au fost construit sau de probabilitatea (marja de eroare) cu care au fost create modelele suprafeţei terestre, atmosferei, ionosferei, elemente de care programatorul are cunoştinţă când s-a apucat de lucru. Din nefericire, în lumea instrumentaţiei virtuale am întâlnit multe astfel de modele destul de aproximative, în diverse domenii practice, livrate cu mare generozitate pe internet fără niciun control decât cel din partea utilizatorului de cele mai multe ori neexperimentat.

Dar, chiar dacă am dispune de un model ideal de exact în rezultatele oferite, utilitatea acestuia ar avea pentru radioamatori un caracter relativ şi subiectiv. Acest model nu va face altceva decât să ne indice cu maximă precizie ce unghi de plecare este necasar. Dacă la acest unghi câştigul antenei este, de exemplu, de -2dB, va trebui să "pompăm" în antenă câţiva kW pentru a trimite un semnal care să acopere pierderile de pe traseu. Ori, acest lucru se practică deja în mod empiric, cu rezultate comparabile. Pentru cine are kW în antenă, comunicaţia se poate realiza şi prin procedee tactice cunoscute precum pândind, urmărind, tatonând dar, dacă nu îi ai, degeaba afli că îţi sunt necesari.

Ce ar fi dacă s-ar putea modifica unghiul de plecare al antenei prin mijloace accesibile, fie ele mecanice, electronice ori combinate? S-a demonstrat cumva că nu este posibil? Cred că prin modificarea unghiului de radiaţie în plan vertical se poate câştiga mai mult pentru DX decât prin mărirea puterii iar acest obiectiv poate constitui o provocare pentru radioamatori. Amintesc doar că amatorii au descoperit undele scurte, SSB cu defazaj, antene performante, deci au arătat că dispun de resurse. Se fac comunicaţii la sute de km prin reflexie pe nori cu fascicul luminos generat de LED-uri de câţiva W [3], de neimaginat acum un sfert de veac, se poate găsi o soluţie şi la modificarea unghiului de plecare în plan vertical prin mijloace mai simple decât dotarea cu un QRO de câţiva kW. În felul acesta, prin baleierea continuă a unui interval de unghiuri de plecare se poate "cădea" pe direcţia cea mai favorabilă (un fel de goniometrare în plan vertical), unde comunicaţia se poate realiza cu câţiva zeci de W în loc de kW. Ecuaţiile lui Maxwell [2] nu şi-au spus încă ultimul cuvânt, poate şi din cauza dificultăţilor care apar la rezolvarea lor. Aşa cum în cei aproape 100 de ani de comunicaţii radio au apărut o varietate de antene individuale sau în arie, nu este exclus să apară şi antena cu reglarea continuă a unghiului de radiaţie în plan vertical. O condiţie este să nu devenim excesiv de tributari schemelor şi modelelor existente şi să căutăm soluţii în principiile fundamentale, tot mai mult date uitării când diseminarea la nivel planetar a informaţiilor şi a tehnicilor de lucru în orice domeniu este pe cale de a se monopoliza, ceea ce cam aduce cu monopolizarea adevărului ştiinţific.

Bibliografie (selectivă).

[1] Creţu Florin, YO8CRZ. Despre unghiul optim de radiaţie al antenelor pentru DX. http://radioamator.ro/articole/view.php?id=938

[2] Orfanidis S.J. Electromagnetic Waves & Antennas, www.ece.rutgers.edu/~orfanidi/ewa 31 August 2010.

[3] Moncur Rex VK7MO, Giles-Clark Justin VK7TW, Sulman Ken VK7DY. Over-The-Horizon Optical Communication. Dubus 4/2008, ISSN 1438-3705, pg. 26.

[4] *** http://radioamator.ro/

[5] *** http://en.wikipedia.org/wiki/Ionosphere

[6] *** Corespondenţă privată cu YO8CRZ

Gheorghe Oproescu-Tavi YO4BKM

Articol aparut la 29-5-2014

10900

Inapoi la inceputul articolului

Comentarii (31)

Postat de Marcel - YO6PMX la 2014-05-29 08:47:17 (ora Romaniei)
Excelent articol! Imi amintesc ce soc am avut acum vreo cateva luni cand mi-am dat in sfarsit seama (de fapt m-a luminat YO6OAH)de ce pentru unele statii trebuia sa intorc antena mai spre N decat era firesc. Am inteles atunci cum e cu geodezica, iar acum o vad excelent explicata aici. Felicitari inca o data!
Marcel - YO6PMX

Postat de Gheorghe Oproescu - Tavi - YO4BKM (yo4bkm) la 2014-05-29 09:06:27 (ora Romaniei)
TNX Marcel YO6PMX! Succes la DX! 73!

Postat de Ioan Mircea Radutiu - YO3AOE la 2014-05-29 11:39:35 (ora Romaniei)
Foarte bun articolul!,multumim si la mai multe-hi!. L-asi ruga mult pe Tavi-YO4BKM sau/si pe Florin-YO8CRZ sa-mi indice un material documentar cit mai bun-detaliat privitor la calculul si variantele practice-concrete ale capacitatilor terminale pentru antenele verticale scurte.Cu multumiri anticipate si cu 73!,Nelu

Postat de Gheorghe Oproescu - Tavi - YO4BKM (yo4bkm) la 2014-05-29 15:39:04 (ora Romaniei)
@Mircea, YO3AOE, am materialul documentar referitor la antenele sectionate (antene verticale puse la pamant si cu capacitate terminala) si iti voi trimite cat mai urgent calculul acestor antene (radiatia in plan vertical, impedanta de radiatie si impedanta de alimentare, cerd ca este cam ce prezinta interes). TNX pentru comentariu, 73!

Postat de Ioan Mircea Radutiu - YO3AOE la 2014-05-29 16:36:00 (ora Romaniei)
Antena verticala scurta o am deja,este vorba despre o BB-7V multi-banda originara de la Diamond,pentru la statia mea mica-mobila pentru lucrul in/din portabil la cort,asa ca m-ar interesa in mod special teoria,calculul si variantele constructive practice-concrete strict ale capacitatilor terminale posibile si utile in acest caz real.Cu stima si 73!,Nelu

Postat de STOLNICU Petrica - YO9RIJ la 2014-05-29 18:22:02 (ora Romaniei)
Un articol de care, sincer, aveam nevoie!
Sanatate multa iti doresc dr OM Tavi! 73! de YO9RIJ Petrica

Postat de Morel - 4X1AD (4x1ad) la 2014-05-29 18:23:58 (ora Romaniei)
Reconfortant material, d-le profesor. De la atata folosire a calculatorului, se mai intampla sa uitam adevarurile fundamentale simple de la baza teoriei antenelor si a propagarii undelor radio. Uneori ne este cam greu sa sa mai gandim si cu capul nostru propriu si sa revenim la metodele manuale. Nu strica nici o reimprospatare a cunostintelor de trigonometrie si geometrie neexersate din liceu sau facultate. Imi amintesc ca acum vreo trei decenii cand am reusit in sfarsit sa-mi ridic primul Yagi rotativ pentru HF, am folosit si eu putin metoda cu ata si doua bolduri pe un glob didactic. Pe atunci, PC-urile erau cu 8086 si 128KB RAM si lucrau cu MS DOS. Doar dupa cativa ani a inceput raspandirea Miniprop-ului si restului de programe de logare/concurs care-ti dadeau pe loc azimutul necesar atat pentru short cat si long path functie de prefixul corespondentului. Apoi, unii din producatorii de rotoare au inceput sa furnizeze si o masca transparenta pentru unitatea de comanda, care avea imprimata pe ea harta lumii centrata in QTH-ul tau, exprimat de acul indicatorului. Dar in loc de trigonometrie trebuia sa cunosti geografie si sa recunosti vizual pozitia tarilor pe harta azimutala care avea deja implementata corectia de sfericitate. Multi din cei obisnuiti cu hartile plane le era cam greu sa recunoasca harta "distorsionata". Dar despre antene si propagare inveti toata viata si nu se termina niciodata. Chiar daca legile de baza ale lui Maxwell nu se schimba, apar multe aspecte noi si nelamurite pentru fiecare generatie de radioamatori la randul ei la. Generatiile actuale au avantajul noilor posibilitati informationale uriase.
In ceea ce priveste precaritatea unor softuri, este adevarat ca programele de simulare/modelare de antene au algoritmi insuficient de dezvoltati, unii plecand la drum cu premise mai superficiale, fapt care duce la limitari si erori inerente. Vorbesc de programele gratuite din domeniul public, desi si variantele lor asa-zise PRO si care costa sute de dolari, au nu putine deficiente. Insa trebuie sa acceptam ca spre deosebire de softurile profesionale extrem de scumpe, in algoritmii creati de radioamatori pentru alti radioamatori nu s-au investit sumele uriase necesare fundamentarii lor complete. Chiar si asa, un program gratis nepretentios, permite niste abordari noi si posibilitati multiple la proiectarea si constructia practica a antenelor noastre modeste. As zice ca sunt de preferat programele noastre asa imperfecte cum sunt, decat lipsa lor care duce la experimentari mai mult pe bajbaite. Extrem de putini poseda abilitatile si cunostintele teoretice necesare calcularii manuale ale diverselor antene. Cred ca lipsa de investie si interes in optimizarea algoritmilor gratuiti provine si din faptul ca pentru aplicatiile noastre de unde scurte acuratetea este necesara mai mult in calculul legaturilor radio de tip point-to-point. Insa in situatia noastra "casnica", cu antene cu lobi foarte largi, si legaturi in majoritate pe baza aleatorie, acuratetea azimutului poate fi mai relaxata. Nu aceiasi este si situatia peste 30MHz si cu cat inaintam spre domeniul microundelor, unde acuratetea este absolut esentiala. Am avut ocazia sa vad softuri pentru telefonia celulara si toate aplicatiile din familia "IEEE 802.11-xxx". Ele sunt de o mare sofisticare si acuratete, chiar daca eu nu am pregatirea si experienta sa apreciez premisele sub care s-au alcatuit algoritmii respectivi. Dar aceste softuri costa enorm si nu sunt destinate decat unor profesionisti bine pregatiti in acest domeniu-nisa. Pretentiile noastre, ale radioamatorilor obisnuiti sunt cu mult mai reduse. Evident ca nu-mi permit sa vorbesc si in numele colegilor nostrii amatori de performanta in VHF/UHF/SHF, ale caror stachete tehnologice sunt mai ridicate.
Am fost multumit de acest material si pentru ca avem prea putine in lb.romana in care vesnicul SWR nu ocupa tot firmamentul. Chestiunea transferului optim de energie intre emitator, fider si antena este foarte importanta si nu trebuie neglijata sub nici o forma. Dar de aici si pana la transformarea problemei SWR-ului intr-un criteriu aproape exclusiv de caracterizare/evaluare al unei antene in vocabularul si mentalitatea unor radioamatori, este cale foaaaarte lunga. Din pacate, prea multi hami fac acest lucru iar problema modului cum este radiata in spatiu energia aplicata la bornele unei antene, este profund neglijata. Ori, chiar daca reusim sa avem pierderi de adaptare cat mai mici posibil pe tot traseul TX-antena, daca antena radiaza defectuos, foarte mult din ce ne-am chinuit sa adaptam se poate risipi inutil de la bornele antenei mai departe in spatiu. Ati reusit sa explicati foarte clar si grafic mecanismul reflexiilor pe straturile ionizate si multe din multiplele aspecte adiacente ale fenomenului. Cred ca mai multi hami inteleg acum mai bine traseul real al undelor emise si complexitatea lui. Acest "knowledge" este necesar pentru toti posesorii de antene, nu numai cei cu sisteme directive costisitoare. Optimizarea modului de radiatie in spatiu al unei antene trebuie sa fie si obiectivul posesorului de LongWire, diversi dipoli, vertical si Delta Loop. Chiar daca la aceste antene posibilitatile de optimizare ale diagramelor de radiatie sunt inerent mai limitate decat la cele rotative mecanic sau electric, ele merita intelese si aplicate pe cat posibil pentru ca nici un amplificator de putere de multi kilowatti nu poate face ceea ce poate da un mic castig suplimentar in gain, F/B, F/S, unghi de plecare/elevatie in plan vertical dar si numarul si forma lobilor de radiatie diversi. Un amplificator poate rezolva partial cresterea probabilitatii unei legaturi radio point-to-point, din pacate doar pe un singur sens. El nu rezolva problema receptiei si aici intervin doar factorii sus-amintiti plus raportul S/N din locatie. Dar pentru ca viata e plina de compromisuri, multi apeleaza la ambele metode: o optimizare cat de cat a antenei in paralel cu folosirea unui amplificator de putere. Din pacate, sunt cam sceptic in privinta aparitiei prea curand a unui sistem care sa permita unui radioamator (fie el si foarte avansat) sa poata anticipa si optimiza traseul undelor, numarul si natura reflexiilor, coroborate cu factorul de relief, traversarea zonelor de uscat sau oceanice. Este necesare o integrare a celor de mai sus cu datele despre indexul solar A si K, fluxul solar, MUF-ul la un loc cu inaltimea si structura straturilor ionizante, raportat la sezon, zi sau noapte plus pozitiile geografice ale celor doua puncte ale comunicatiei point-to-point. In plus, toate aceste date trebuie furnizate utilizatorilor printr-un sistem complex de culegere si diseminarea a datelor. Mie mi se pare o misiune absolut sisifica, de o complexitate care poate fi abordata la ora actuala doar de 2-3 armate din lume. Nu spun ca este o imposibilitate tehnica pentru ca acest sistem exista de mai mult de 2 decenii, dar a costat multe miliarde iar mentinerea lui in functiune zi de zi este si ea o misiune extrem de costisitoare. Pentru radioamatori, este un exercitiu cerebral minunat, fara indoiala posibil teoretic dar imposibil de implementat practic.
In aceste conditii, cred ca cei pasionati de unde scurte trebuie inca sa se multumeasca cu mijloacele clasice, din batrani. Marirea considerabila a distantei comunicatiilor intre 3-30MHz trebuie sa i-a in considerare micsorarea pe cat posibil a unghiului de plecare in plan vertical si o cat mai buna intelegere a mecanismelor de propagarea a undelor radio. Evident, acest unghi de plecare in plan vertical nu trebuie folosit ca o lozinca in sine, ci trebuie nuantat, functie de multi factori. Ca si in alte domenii, generalizarile nu au mare relevanta si toate cazurile trebuie abordate specific. Astazi, controlul asupra unghiului de plecare al undelor se poate face prin: preferarea antenelor care prin conceptie si constructie au un unghi mai redus decat altele; amplasarea lor la inaltimi corespunzatoare scopului urmarit; folosirea sistemelor de antene multiple etajate (stack) care pot acoperi prin comutare zone de interes diverse. Acestea din urma sunt apanajul unei fractiuni de procent din numarul radioamatorilor si necesita nu numai multi bani si spatiu rural, ci si capabilitati conceptuale, abilitati de calcul si modelare/simulare a sistemului. Mai neaos spus: nu este suficient sa ai bani ca sa poti reusi sa imaginezi un astfel de sistem. Includ aici si partea de mecanica- rezistenta materialelor. E bine de stiut ca marirea inaltimii antenelor acolo unde este practic posibila, aduce si anumite dezavantaje: desi unghiul de plecare in plan vertical scade poate chiar la numere cu o singura cifra, numarul de lobi creste vertiginos ceea ce duce in paralel si la un anumit grad de risipa de energie. Esentialul este pastrarea unui raport optimizat intre inaltime si numarul si forma lobilor aparuti.ca urmare a mariri inaltimii. Adica, trebuie sa pastreze un balans intre castigul potential si pierderile paralele prin "risipa". Acesta este un subiect rar abordat, dar n-am sa-l dezvolt acum, intrucat comentariul a devenit si asa prea lung. Oricum, este clar ca interpretarea prin generalizare a maririi inaltimii antenelor respectiv a cresterii unghiului de plecare in plan vertical, este total neproductiva.
Multumiri pentru minunatul articol, YO4BKM si asteptam mai multe la fel de interesante. Eventual si un "Antenna Handbook" in lb.romana. Multumiri reinnoite si lui YO8CRZ pentru cartea "Radiotehnica" si restul articolelor (in special: http://radioamator.ro/articole/view.php?id=938 si http://www.radioamator.ro/articole/view.php?id=926 ). Reamintesc ca aceasta carte nu se va reedita la nesfarsit iar cei care n-au comandat-o inca, sa se grabeasca s-o faca la: http://www.radioamator.ro/misc/formular-carte.php . Nu, nu primesc comision de la YO8CRZ, hi.

73
Morel
4X1AD
ex.YO4BE.

Postat de Gheorghe Oproescu - Tavi - YO4BKM (yo4bkm) la 2014-05-29 23:46:33 (ora Romaniei)
@4X1AD, sunt impresionat de extrem de cuprinzatorul comentariu, care arata o exceptionala documentare in domeniu. Imi sunt foarte clare dificultatile si eforturile uriase care se cer pentru a oferi o optimizare a traseului undei radio intre doua puncte alese. Dar, ca sa fiu sincer, cand am putut descifra in toate detaliile complicatul mecanism dupa care functioneaza mult prea comunul de acum GPS, imi venea sa zic precum taranul care vede pentru prima data o girafa: "asa ceva nu exista!". Asigurarea unei erori de cativa metri la utilizator presupune cunoasterea aproape fara erori a vitezelor undelor radio prin orice zona cuprinsa intre suprafata terestra si satelitii de navigatie, determinarea acesteia se repeta la intervale de maxim cateva secunde iar valorile gasite sunt transmise in permanenta navigatoarelor GPS pentru a le folosi in calculele necesare aflarii pozitiei. Si nu numai atat, au mai trebuit rezolvate sincronizarea la picosecunda a semnalelor transmise de sateliti, telemetrarea continua a pozitiei fiecarui satelit cu erori mai mici decat erorile de pozitionare oferite de navigatorul GPS si altele de acest fel. Ca si internetul, navigatoarele GPS au fost dezvoltate de armata in folosul ei exclusiv, au costat enorm, dar s-au extins rapid in lumea civila cand au putut aduce beneficii. Exista, asadar, o buna baza de date privind caracteristicile atmosferei oriunde in jurul globului, plus o cartografiere cu mare precizie a suprafetei terestre, macar la nivelul hartilor din navigatoarele GPS, deci "girafa" optimizarii traseelor radio poate prinde contur. Pentru asta este necesar sa se mai rezolve cateva "banalitati": elaborarea unui soft specializat care sa aibe continuu acces la bazele de date oferite de sateliti, asa cum exista deja softurile care ofera harti ale frecventelor critice actualizate la fiecare 5 minute. Algoritmii pentru modelarea pe calculator nu ridica probleme, problema este la gestionarea unui volum urias de date, pentru care un simplu PC nu face fata. Un navigator GPS primeste informatii strict punctuale pe care le prelucreaza repede, un sistem de gestionare a unui volum mult mai mare de informatii la nivel planetar necesita statii de stocare si calcul la care beneficiarii se pot doar conecta, in niciun caz nu le pot detine. Iar radioamatorii interesati de DX reprezinta o fractiune infima in raport cu utilizatorii de GPS, astfel incat contributia lor financiara la un sistem functional global este neglijabila in raport cu perturbarea pe care ar aduce-o exploatand sistemul in parteneriat cu profesionistii. Asa cum bine aratai, ne raman execitiul cerebral, compromisurile, diseminarea experientei -buna sau mai putin buna- si, cine stie, o suficienta acumulare de tip cantitativ poate duce la saltul calitativ de care am putea beneficia. Imi tot vin in minte lucruri citite candva. Daca acum 200 de ani i s-ar fi cerut unui bastinas din vreun trib inapoiat sa construiasca un sistem de comunicatii care sa acopere o arie de sute sau mii de km, poate ca s-ar fi gandit la un tam-tam mare cat un conac, acum folosim undele radio. Leonardo da Vinci scria in notitele sale ca ingineria acelor timpuri a ajuns la perfectiunea maxima care nu mai poate fi intrecuta, putand construi orice arma de razboi oricat de cumplita. Nu-si imagina armamemntul de azi. Marconi a folosit emitatoare de zeci sau sute de kW pentru un trafic radio care acum necesita zeci sau sute de W. Astfel de exemple ma fac sa afirm ca a fi excesiv de tributar schemelor sau modelelor existente este cel mai daunator lucru. De aceea apreciez deosebit invitatia la exercitiu cerebral facuta de 4X1AD. 73!

Postat de Florin - YO8CRZ la 2014-05-30 07:03:28 (ora Romaniei)
Binevenit acest articol, intr-un domeniu prea putin abordat la noi. Ma bucur ca in mod direct sau indirect am cauzat dezbaterea, cred ca este benefica pentru un numar mare de radioamatori. Problemele legate de propagare sunt destul de complexe si in multe cazuri trebuie sa facem simplificari pentru a putea merge mai departe cu intelegerea. In mod cert articolul scris de mine depre unghiul optim de radiatie a antenelor la DX sau chiar cele scrise in cartea Radiotehnica nu pot acoperi decat partial o problematica atat de vasta cum este propagarea. Pe unii nu-i intereseaza, insa pentru cei care vor sa stie si sa inteleaga, cred ca au au acum la dispozitie macar elementele de baza in materie. Cat despre simularile de propagare, programele ce folosesc nucleul VOACAP, care sunt disponibile pentru radioamatori, dau in general rezultate cu acuratete rezonabila pentru propagarea medie. Asta inseamna ca nu iau in considerare varfuri scurte de propagare, indicii ionosferici la nivel orar sau cazurile de propagare speciala gen ductie intre straturile ionizate. Fireste ca exista si programe care pot face asta ...insa nu gratis. Tin sa amintesc ca relieful terstru a fost cartografiat 3D cu mare rezolutie de NASA la inceputul lui 2000, si a fost pus la dispozitie publica (insa cu o rezolutie ceva mai redusa). Programele serioase iau in considerare relieful. Programul HEFTA este singurul pentru radioamatori din cate stiu, care foloseste doar relieful din zona antenei pana la 4-5Km departare, insa acesta nu este decat tangential un program de predictie. Oricum cand e vorba de propagare, ca radioamatori, putem discuta doar in termen statistici… Uneori predictia e corecta alte ori nu… Chiar si asa, pot spune scepticilor ca am reusit cateva DX-uri grele, folosind predictia propagarii. Am mers pana acolo incat am plecat in pauza de masa de la servici acasa pentru ca programul de propagare spunea ca atunci este momentul optim pentru a lucra un DX rar…si a mers…si nu doar odata ! Sau sculat la 4:00AM pentru ca era momentul optim in banda de 40m… Avand in vedere ca folosesc de obicei putere destul de redusa si nici nu ma numar printre cei care pot petrece un timp nelimitat in fata statiei, trebuie sa suplinesc asta cu ceva…hi,hi, altfel asa cum spunea Pit- YO3JW, stai la coada pana cand cei care pot si au cu ce, si-au facut plinul… 73 de Florin YO8CRZ.

Postat de Cristi - YO3FFF la 2014-05-30 15:28:09 (ora Romaniei)
Citez din articol:
=============
"Ce ar fi dacă s-ar putea modifica unghiul de plecare al antenei prin mijloace accesibile, fie ele mecanice, electronice ori combinate? S-a demonstrat cumva că nu este posibil?"
=============

Aveti raspuns la aceste intrebari?
Daca da, puteti va rog sa exemplificati cu o realizare practiva a unei astfel de antene, sa zicem pentru frecventa de 7MHz?

Altfel, desi articolul nu aduce nimic nou, este binevenit in zona radioamatorismului YO, si asa pe cale de disparitie.

Succes.

73 de YO3FFF
Cristi

Postat de Gheorghe Oproescu - Tavi - YO4BKM (yo4bkm) la 2014-05-30 15:42:36 (ora Romaniei)
@Cristi, YO3FFF, raspunsul pe care il astepti este imediat in continuarea extrasului pe care il citezi. Cat priveste daca ceva este sau nu este nou, depinde de experienta fiecaruia. Daca o persoana este detinatoarea unor informatii pe care le disemineaza, este evident ca cel putin pentru ea nu mai sunt noutati. Si, cum comunitatea noastra numara multi membri experimentati, se confirma caracterul relativ al noutatii. Altceva este in cazul unor realizari inedite, inovatiilor sau inventiilor, care cu siguranta vor fi apreciate in unanimitate. 73!

Postat de Morel - 4X1AD (4x1ad) la 2014-05-30 18:34:50 (ora Romaniei)
@YO3FFF: Cristi, ideea este realizabila tehnic. Sa nu vorbim de sisteme de antene etajate unde modificarea unghiului de plecare in plan vertical se poate face cu un simplu comutator de antena care sa aleaga intre antenele amplasate la diverse inaltimi. Dar hai sa vorbim de cei multi care nu-si pot permite o astfel de investitie uriasa. Sa luam exemplul dorit de tine, intr-un scenariu tangibil: o antena pentru 40m. Un Inverted Vee de 2x10.2m la o inaltime de 10m (capetele la 3m de sol, balun 1:1), are un unghi de plecare de 65de grade (f=7050KHz, SWR=1:1.4, Ga=4.7dBi). Aceiasi antena inaltata cu doar 5m, cu capetele la 8m de sol, are un unghi de plecare de 48 de grade (SWR=1:1.9, Ga=4.4dB). Pentru 5m in plus, ai reusit o reducere de aproape 20 de grade. Ca sa nu batem campii cu simple teorii, cum s-ar putea asa ceva realiza practic? Ce-mi vine acum in minte este un suport fix sau telescopic (cine poate) de 15m inaltime, prevazut la varf cu un scripete de care este prins cu o cordelina balunul si antena permitand ridicarea sau coborarea antenei cu 5m. Evident, schimbarea se face manual, ceeace face ideea mai aplicabila la un Field Day, concediu, camping etc.. Sau cine e binecuvantat cu curte. Cele 17 grade diferenta in 7MHz inseamna foarte mult si pot reprezenta 1,2 poate chiar 3 reflexii economisite, adica mii de kilometri in plus. Cred ca YO4BKM cu abilitatile sale de calcul iti poate avansa DEMO un numar urmat de trei zerouri ca sa ilustreze valoarea reflexiilor, desi un calcul foarte exact este greu de facut pe o situatie nespecifica (spre deosebire de comunicatiile de tip point-to-point amintite de YO8CRZ, care-ti permit un grad mare de probabilitate a predictiei).

73
Morel,
4X1AD
ex.YO4BE

Postat de Popa Gheorghe - YO2MTG la 2014-05-31 11:12:01 (ora Romaniei)
Felicitari domnilor pentru articol, explicatii si pentru comentarile aparute, foarte pertinente si la subiect.
73 de YO2MTGigi

Postat de Miki - YO5AJR (yo5ajr) la 2014-06-03 16:22:55 (ora Romaniei)
Ori cat m-am stapanit sa nu postez comentariu la acest articol - na ma pot stapani. Articolul lui Tavi este un veritabil "ignition" al imaginatiei radioamatorului. Recunosc ca am construit foarte multe antene da a lungul anilor bazandu - ma pe un anumit "filling" greu de explicat. Dorinta mea secreta de decenii ca plecarea electronilor din antenele mele sa pot vizualiza ca si fileurile de aer in tunelele aerodinamice, in imaginatia mea mereu ma gandeam ca solul sub antenna este o oglinda perfecta din care cauza si contragreutatile intinse plasam de multe ori la distanta fata de proiectie pe varticala al radiantului influentand directiile intr-un sens sau altul. Am cautat harti cu sectiune verticala a locului geografic pe directii, morfologia solului si alti factori care sunt atat de multe ca te ametesti. Cum nici - o data nu ma pot multumi de receprie am incercat K9AY - EWE, Bew si am costatat fenomene care cauta raspuns (dar nu mai am mult timp....h) Lucrand preponderent in 160m dar si pe 40m consta perioade in care pe ant. de TX nu pot receptiona corespondentul iar pe EWE vine curat - asta ar fi normal, nu e nurmal insa cand fenomenul e invers, adica pe EWE nu iar pe ant TX da. Este o teme extrem de vasta care nu te lasa sa te imbatranesti prematur tinand in miscare neuronii proprii. Multumesc Tavi - multumesc tuturor. 73/DX yo5ajr Miki

Postat de Nicolae Crisan (Nicu) - YO5OUC la 2014-06-07 16:26:33 (ora Romaniei)
O foarte buna descriere si un limbaj tehnic de exceptie. Singurul regret e legat de faptul ca nu am citit mai devreme articolul. Legat de problema ridicata mi-as permite un mic comentariu. Problema controlului caracteristicii de radiatie a fost rezolvata in domeniul microundelor acolo unde se poate vorbi cu adevarat de arii de antene "electronically steerable". Aplicatii specifice sunt la radarele moderne unde antena nu se roteste sau la sistemele MIMO. Aici in US metoda aplicata la antenele array prin controlul fazelor pentru fiecare antena nu functioneaza. Aceasta teorie aici devine inoperanta din cauza distantei de minim lambda/2 dintre elementele ariei de antene. In 80m ar fi nevoie de o distanta minima de 20m ceea ce complica mult lucrurile in contextul amatoricesc in care ne desfasuram noi. In literatura se vorbeste tot mai mult de potentialul ne-explorat 100% al antenelor nerezonante cu unda progresiva. Din aceasta grupa face parte antena long wire pe care noi o folosim intensiv. Aceste antene sunt directive, iar caracteristica de radiatie numarul si forma lobilor depinde de frecventa. Astfel la frecvente diferite unghiul a1 se poate modifica norocos. Pentru o frecventa fixa mi-as permite s-a aduc in discutie rolul radialelor la antena Marconi ce pot controla unghiul de plecare a1 din felul in care fac un unghi cu planul orizontal. Daca radialele sunt lasate in jos sub unghiul de 45 grade a1 este aproape zero, iar daca fac un unghi de 0 grade atunci a1 este de aprox 36 grade. As sugera un sistem mecanic ce modifica unghiul radialelor sau trei antene verticale cu unghiuri diferite pentru radiale. In cazul unui sistem mecanic de control lungimea radialelor poate fi redusa prin utilizarea trap-urilor pe fiecare. Astfel se reduce greutatea lor.

Cu multa prietenie.
Nicu - YO5OUC

Postat de Gheorghe Oproescu - Tavi - YO4BKM (yo4bkm) la 2014-06-07 18:25:08 (ora Romaniei)
@YO5OUC, îţi mulţumesc pentru comentarii şi dă-mi voie la câteva completări. Antena long wire este o antenă rezonantă. Orice fir care are cel puţin un capăt izolat, unde este nod de curent, face ca pe lungimea lui să se formeze unde staţionare începând de la nodurile din capete sau de la un singur nod la long wire. Dacă lungimea antenei este în relaţie cu lungimea de undă (semiundă la antenele cu două capete izolate, sfert de undă la antenele cu un capăt izolat) antena se numeşte acordată. Antena cu unde progresive este antena cu rezistenţă terminală acolo unde capatul este izolat la long wire, precum atena Beverage. Cât priveşte modificarea unghiului de plecare în plan vertical pentru HF, se cunosc destule metode mecanice, electronice, mixte, dar care sunt tributare aceloraşi reguli: o antena orizontală, cu unde polarizate orizontal, va avea fie un singur lob de radiaţie la un unghi mare faţă de orizontală, fie mai mulţi lobi ca să poată radia şi la unghiuri mici, acestea depind de înălţimea faţă de sol; o antenă verticală pusă la sol, cu unde polarizate vertical, are numai unghiuri mici de plecare dacă dorim un singur lob, fie o paletă de unghiuri dacă acceptăm mai mulţi lobi, acestea depind de înălţimea antenei. Deosebirea apare deoarece undele polarizate vertical pierd o smiundă (sau un pi/2 din fază) la reflexia pe sol, undele polarizate vertical nu pierd această fază. În ariile de antene se exploatează tot astfel de fenomene, cu unde convenabil defazate. Soluţia de viitor este o altă schemă de antenă, cu totul deosebită de ce se ştie, probabil aşa aşa cum este radioul faţă de telefonul cu fir. De aceea am recomnadat că nu este bine să rămânem tributari soluţiilor existente. 73

Postat de Gheorghe Oproescu - Tavi - YO4BKM (yo4bkm) la 2014-06-08 07:31:20 (ora Romaniei)
Corectie mai sus: undele olarizate orizontal pierd o smiunda la reflexie, din nou graba si-a spus cuvantul! 73!

Postat de Nicu - YO5OUC la 2014-06-08 13:24:09 (ora Romaniei)
Iti multumesc Tavi pentru raspuns si completari. Sunt de acord cu ce spui doar ca eu cred ca incadrarea antenei long wire intr-o categorie sau alta este destul de dificila. Asa cum spui antena Beverage terminata cu sarcina adaptata se apropie mai mult de categoria antenelor nerezonante. Orice antena de-a lungul careia nu se formeaza noduri si ventre este practic nerezonanta. Practic din cauza adaptarii de la capat nu exista unda reflectata la Beverage. Pentru linii lungi se intimpla la fel pentru ca unda este radiata de-a lungul liniei si daca lungimea este destul de mare in raport cu lambda (adica nu e linie stub) unda ce ajunge la capat este aproape zero deci nu se mai intoarce. Ce vreau sa spun e ca long wire-ul se comporta ca un element nerezonant la frecvente mari pentru care este indeplinita conditia asta si rezoneaza la frecventele mici asa cum spui tu. De exemplu un long wire de 80 m rezoneaza pe 3,5 si 7 MHz si pe analizor RL-ul este mare (sau dip-ul) pe cind la frecvente mai mari de 10 MHz SWR-ul sta frumos in 1:1. Eu nu am folosit long wire si nu pot sa confirm decit teoretic ca asa ar trebui sa fie. Poate ca cei care au long wire sa-mi confirme sau infirme afirmatia aceasta. Inca o data sunt de acord cu ce ai scris doar ca nuantele legate de interpretari pot lungii prea mult comentariul si am preferat sa o clasific ca nerezonanta fara sa mai adaug ceva sau sa nuantez cumva afirmatia. In ceea ce priveste alte modele de antena cu totul diferite de abordarile clasice de acum 40-50 de ani eu personal nu am vazut sau auzit. Ar fi insa interesant sa aflu poate chiar aici cine stie dintr-un articol scris pe radioamator.ro.

Postat de Gheorghe Oproescu - Tavi - YO4BKM (yo4bkm) la 2014-06-08 15:57:22 (ora Romaniei)
Nicu, YO5OUC, sunt de acord pana la un punct. Anume ca longul sa fie atat de lung incat, datorita pierderii de energie prin radiatie, cu mult inainte de capatul izolat sa nu mai existe curent prin fir si nici noduri sau ventre. Eu am folosit un long de 42 m vreme de peste 20 de ani, pana acum 6-7 ani in urma, o consider drept cea mai buna antena filara din cate am avut, aveam aparatura HM cu QRO cu tuburi (80W input) si drept adaptor clasicul filtru PI, am lucrat toata lumea pe toate benzile, in QRP (3W) am lucrat toata Europa pe toate benzile. Manevrand filtrul PI observam ca antena este rezonanta (existau puncte clare de acord) chiar si in 10 m (8 semiunde). Dar este pretentioasa la instalare deoarece trebuie sa plece direct din etajul final si sa nu faca unghiuri mai mici de 120-150 de grade. Cand mi-am schimbat QTH-ul, s-au schimbat si conditiile. Alimentarea unui long prin linie de alimentare nu este buna, nu mai este long ci orice altceva. Dar retine regula, daca pe lungimea unei antene se formeaza cel putin un nod de curent datorita constructiei antenei, antena este sigur rezonanta. Nu stiu cat de bun este analizorul pe care-l folosesti, eu am aratat ce am constatat experimental si nu numai eu. Pe de alta parte, nici nu afirm ca am vazut antene diferite de cele clasice, ele trebuie inventate. Lucrez acum la un model de antena cu polarizare variabila electronic, deci si cu modificarea unghiului de plecare, numai ca este extrem de complicat, trebuie sa refac toate formulele plecand de la expresiile care definesc vectorii potential magnetic A(r) pe care sa ii integrez apoi pe conductorii noului tip de antena, se lucreaza cu integrale transcendente din functii de variabila complexa pe conductori cu configuratie neclasica. Si ce ti-am trimis pe e-mail, tot prin aceleasi metode, personale si originale, le-am obtinut. Le-ai incercat? Sunt 100% corecte deoarece cele doua tipuri de antene le-am exploatat si eu, acum am un Windom HM pentru toate benzile si este in concordanta cu modelul meu. Pe aceste considerente nu cred in povestile care arata ca cu un singur balun se poate adapta un Windom pe orice banda (poate ca cu cate un balun pe fiecare banda) si nici ca se poate contrui un Windom care sa se adapteze fara ATU. 73!

Postat de Morel - 4X1AD (4x1ad) la 2014-06-09 11:33:19 (ora Romaniei)
@YO5OUC: te citez: "De exemplu un long wire de 80 m rezoneaza pe 3,5 si 7 MHz si pe analizor RL-ul este mare (sau dip-ul) pe cind la frecvente mai mari de 10 MHz SWR-ul sta frumos in 1:1."

Nicu, cum arata un astfel de longwire ? Ma refer la lungimea totala si raport intre partea orizontala si cea verticala ? La ce inaltime de la sol ?

73

Morel

4X1AD

ex.YO4BE

Postat de Nicu - YO5OUC la 2014-06-09 12:31:26 (ora Romaniei)
raga Morel, nu stiu ce sa-ti spun pentru ca repet nu am lucrat practic cu long wire. Teoretic orice fir orizontal aflat la o distanta de minim lambda fata de pamint rezoneaza pe frecvente ce sunt multiplii intregi de lamda pe doi. Daca firul are 80 m rezoneaza si la 3.5 MHz (2*lamda/2) cel mai bine insa la 1.8 (lamda/2) din ce in ce mai slab la 7MH, 14MHz din cauza atenuarii pina cind la frecvente mai mari nu mai rezoneaza. Unda directa se tot atenueaza, iar cind ajunge la capat e aproape zero deci ce se intoarce e nesemnificativ. Vroiam sa zic ca daca din cauza lungimii unda reflectata e aproape zero atunci SWR-ul e 1:1 la orice frecventa deci linia e nerezonanta. La orice linie rezonanta SWR-ul tinde la 1:1, RL la infinit (cind apare dipul), iar la alte frecvente SWR-ul e mare si RL-ul aproape de zero. De exemplu un cablu coaxial foarte lung cu pierderi devine nerezonant chiar daca se termina in gol sau dezadaptat. SWR-ul masurat este 1:1 pentru orice frecventa pentru ca unda reflectata nu mai ajunge inapoi la statie. Am vrut sa zic ca asa ar trebui sau asa inteleg eu ca ar trebui sa functioneze un long wire. Intr-o carte publicata la Editura Tehnica de catre d-ul ing. Ianculescu se specifica ca un long wire trebuie sa aiba lminim=lamda caz in care are un cistig de 0.5 dB, dar in cazul corect in care l=8*lamda cistigul creste la 6.2 dB. Draga Morel, poate ca nu am dreptate, dar poate ca am. La 8*80 m banuiesc ca antena va putea fi folosita la orice frecventa >3.5MHz, fiind o antena cu unda progresiva pentru orice frecventa mai mare decit c/lambda.Cei ce au un long wire pot sa confirme sau sa infirme ceea ce eu simt.Asta desigur daca antena nu e influentata prea mult de sol. Eu personal cred ca un long wire nu se comporta ca atare decit la frecvente mai mari de 14 MHz, iar la frecvente mai mici devine rezonant. Cine ar putea monta practic o antena la 80m fata de sol. Blocul meu are numai 30m si e cu 10 etaje.
Poate ca nu am dreptate sau poate ar fi mai bine o dezbatere pe aceasta tema. Pro & Contra hi.
73! de Nicu

Postat de Gheorghe Oproescu - Tavi - YO4BKM (yo4bkm) la 2014-06-09 13:53:49 (ora Romaniei)
Scuze, mesajul anterior a plecat trunchiat, nu ştiu din ce cauză, îl reiau.
@YO5OUC ai complicat rău lucrurile de nu se mai înţelege nimic. Pe de o parte spui că nu ai lucrat cu long, pe de altă parte nu crezi în ce spun cei care l-au folosit în extrem de diverse condiţii sau l-au cercetat sub toate aspectele, teoretice dar şi practice. Mai întâi fixez câteva puncte: 1.Am lucrat cu long până la 8 semiunde şi se comporta ca antenă rezonantă care se acorda din filtrul PI după indicaţiile reflectometrului şi curentului anodic; 2.Pierderile produse prin curenţii induşi în sol nu sunt atât de mari încât să atenueze semnificativ unda din firul antenei, una din cărţile mele de căpătâi pe care o indic şi la bibliografia articolelor mele spune clar acest lucru. 3.Câştigul unui fir creşte cu lungimea sa relativă, exprimată în lungimi de undă, cartea de care vorbeam mai sus arată că este posibil să funcţioneze şi la 12 lungimi de undă unde câştigul ajunge la 8 dB; ceva asemănător vei vedea la antenele Windom multiband, pe care ţi le-am trimis pe e-mail (aştept un răspuns!), câştigul nu este influenţat de locul unde este alimentat firul; 4. Un fir orizontal rezonează (în el apar unde staţionare) pentru orice lungime a sa (confunzi firul rezonant cu firul acordat) indiferent înălţimea faţă de sol, firul devine acordat pentru multipli de semiunde sau sfert de undă, depinde de câte capete libere are, aici are o inflenţă înălţimea faţă de sol dar corelată şi cu grosimea lui. Faci o precizare ambiguă, "antena cu unda progresiva pentru orice frecventa mai mare decit c/lambda", despre ce lambda este vorba? Mai departe, ce rol atribui înălţimii de 80m de sol şi asupra cărui parametru al antenei? Iarăşi neclar. Cât priveşte dezbaterea, aici este clar: nu-şi are rostul deoarece problema longului este rezolvată în cărţile de specialitate, în teoria antenelor descrisă excelent în http://www.ece.rutgers.edu/~orfanidi/ewa, în practica celor care l-au folosit iar deciziile pro & contra în ştiinţă nu se iau cu majoritate de voturi. Dacă nu crezi pe alţii, vei fi mult mai mult în câştig dacă vei căuta răspusurile dorite în experimente proprii decât în cine ştie ce analizoare care dau erori sau pe care nu le stăpâneşti, asta dacă literatura de specialitate nu te mulţumeşte sau nu o înţelegi. Oricum ar fi, radioamatorismul (dar şi radioamatorul) nu pot fiinţa fără experiment şi practică. 73!

Postat de Gheorghe Oproescu - Tavi - YO4BKM (yo4bkm) la 2014-06-09 13:58:24 (ora Romaniei)
Rog pe N2YO să şteargă mesajul care aplecat trunchiat, cel care are ca dată şi oră 2014-06-09 13:49:29 (ora Romaniei), dar şi acest mesaj de informare. Nu ştiu de ce, când scriu mesaje mai lungi sau care durează mai mult ca să le aranjez, nu mai recunoaşte codul de control pe care-l preiau din pagina, aşa s-a întâmplat şi cu mesajul care a sosit trunchiat, am reintrodus codul şi mesajul s-a transmis trunchiat. 73!

Postat de Nicu - YO5OUC la 2014-06-09 15:59:13 (ora Romaniei)
Va multumesc pentru lamuriri.
73! Nicu - YO5OUC

Postat de Nicu - YO5OUC la 2014-06-09 20:29:57 (ora Romaniei)
Draga Tavi - Orfanidis e unul din autorii mei preferati dupa care am facut si simulari de antene in MATLAB (dupa exemplele ce insotesc cartea lui). Totusi in carte sunt descrise antenele Beverage si incadrate corect la leaky-wave antenna nu antenele long wire. Inainte de Beverege a fost insa long wire ce este incadrata tot corect in categoria antenelor cu unda progresiva de asta data de catre un guru in domeniul antenelor (Balanis). Antena leaky-wave face parte dintr-o categorie mai mica, tot a antenelor cu unda progresiva. Antena long wire este si ea incadrata in categoria antenelor cu unda progresiva, dar lenta, de catre acelasi guru al antenelor Balanis (in cartea sa de referinta Antenna Theory - Analisis and Design editia a III-a din 2005 -vezi pg. 551). Iata ce scrie Balanis:

"An example of a slow wave traveling antenna is a long wire, as shown in Figure 10.1.
An antenna is usually classified as a long wire antenna if it is a straight conductor
with a length from one to many wavelengths. A long wire antenna has the distinction
of being the first traveling wave antenna."

Antenele cu unda prograsiva sunt in general nerezonante. Atacul la capatul antenei long wire trebuie sa fie in tensiune pentru ca au rezistente mari la capete (200-300 ohmi):

rez_capat = 138 log10(4h/d)

si rez_capat depinde de inaltimea de la sol h si diametru fir d.
Sigur antena este orientata in plan orizontal deci paralela cu pamintul.

Am spus ca antenele cu unda progresiva deci si antena long wire sunt clasificate in general ca nerezonante. Iata cazul in care antena long wire poate rezona dupa Balanis:

"Resonant wire antennas are formed when the load impedance of Figure 10.1(a) is not
matched to the characteristic impedance of the line. This causes reflections which with
the incident wave form a standing wave."

Deci daca la un capat e conectata o sarcina dezadaptata apar rezonante din cauza undei reflectate. In caz de adaptare nu rezoneaza deci daca la capat atac antena cu un generator cu impedanta de 50 ohmi printr-un baloon cu transformator de impedanta adaptat, aceste rezonante dispar. Daca energia undei este radiata inainte de a ajunge la celalalt capat nu apare unda stationara deci nici rezonantele. Se comporta ca o linie adaptata ce absoarbe toata puterea undei directe.

Iata in ce cazuri mai poate rezona un long wire zice Balanis:

"Resonant antennas can also be formed using long wires. It can be shown that for resonant long wires with lengths odd multiple of half wavelength (l = nλ/2,
n = 1, 3, 5, . . .)"

Rezistenta ei de radiatie va fi in acest caz de:

Rr = 73 + 69 log10(n)

deci cu cit mai lunga cu atit mai bine si iata de ce 8*lamda nu rezoneaza pentru ca 8 e par si probabil din cauza asta se recomanda 2,4,6,8 nu 1,3,5,7 lambda pentru ca numai pentru impar ar rezona.

Acum cred ca e clar de ce am folosit termenul de in general antenele cu unda progresiva nu rezoneaza. Nu rezoneaza daca sunt folosite corect!

Draga Tavi, in general nu vreau sa fac polemica si nu pun etichete nimanui. Oricine trece prin etapa neintelegerii unui fenomen si termina cu etapa intelegerii lui daca insista. De aici si pina la a afirma despre cineva ca nu intelege ce citeste e o cale mai lunga. Cred ca amindoi am trecut de mult de faza neintelegerii prin partile esentiale.
Nu am pretentia ca sunt nici nestiutor, dar nici atotstiutor.

In stiinta nu se voteaza e adevarat, e de ajuns un simplu argument bun. Iata unul!

Balanis spune ca antena long wire a fost prima antena cu unda progresiva. Antenele, se stie ca se impart in doua categorii mari:

Rezonante (cu unda stationara)
Nerezonante (cu unda progresiva - Balanis pg. 550
"traveling wave or nonresonant antennas")

Balanis zice asa: antena long wire este prima antena cu unda progresiva (deci nerozanta in general), dar poate rezona in anumite conditii (de dezadaptare sau a unei lungimi multiplu impar de lamda).

Balanis e cea mai buna referinta stiintifica in antene, crede-ma pe cuvint.

Antena Beverage este un long wire scurtat, lucru permis de sarcina adaptata la capat si ea, nerezonanta. Apare dupa antena long wire ca o imbunatatire scurtata a ei.

Intentia mea nu este sa dezinformez ci sa inteleg cit mai multe. Nu am lucrat cu long wire, dar nu inseamna ca nu am citit despre aceasta.

Daca numai cei ce au experimentat au dreptul la o opinie atunci retrag cele spuse de mine mai sus desi nu cred ca din ceea ce s-a scris aici, cineva a ramas confuz ci din contra, cred ca, a apreciat calitatea articolului tau.

Ce ar trebui sa inteleaga cititorul din afirmatia mea referitor la antenele fir foarte lung e ca daca teoretic un fir foarte lung neinfluentat de pamint e parcurs de o unda progresiva de curent sau tensiune, acesta va fi radiata de-a lungul sau, iar puterea semnalului se tot pierde pe masura ce acesta strabate firul. Daca e suficient de lung sau puterea injectata suficient de mica, semnalul nu va mai ajunge pina la celalalt capat si nu va fi nici o reflectata (responsabila de rezonantele antenei). Aceste antene sunt nerezonante numai daca unda reflectata nu exista sau apar numai unde directe ce au toate acelasi sens si sunt in faza. Numai asa e long wire daca e nerezonanta.

Sau altfel pentru cei confuzi; un fir coaxial foarte lung, in gol, masurat la un capat nu se va comporta niciodata ca un rezonator decit daca nu are pierderi. Pune tu cititorule un SWR-metru dupa statie si masoara SWR-ul, cind linia coaxiala e de circa 100 m, in gol, dar cu pierderi. Injecteaza doar 1W si cred ca stii ca ai sa masori SWR de 1:1 indiferent de frecventa. Linia se va comporta cam ca un long wire adevarat numai ca, puterea se transforma in caldura. Nu vei masura nici o rezonanta. Totul va suna bine cind puterea de RF nu ajunge la capatul celalalt al liniei. Finalului ii va placea.
De rezonante nici nu poate fi vorba.

In loc de incheiere vreau sa remarc ca uneori cineva poate masura rezonante la un long wire. In acest caz antena nu lucreaza asa cum a fost proiectata. Ori e prea scurta ori scurtuta dar miltiplu impar de lambda ori puterea injectata e prea mare ori la un capat e o dezaptare. Uneori antena ta long wire va fi rezonanta, dar nu se vrea asta. Cei care au proiectat-o au vrut sa fie nerezonanta, dar tu trebuie sa o folosesti corect adica lungimea ei sa fie de 8*lambda sau daca nu poti sa o faci suficient de lunga pune o sarcina adaptata la capat sau nu pompa prea multa putere in antena ca devine rezonanta si nu vrei asta. Vrei un long wire.

Cred ca ar trebui sa ne oprim aici.
E greu sa faci un long wire sa lucreze ca un long wire. De multe ori devine rezonator si atunci nu mai lucreaza asa cum a fost gindit. Din antena cu unda progresiva (nerezonanta) devine rezonator cu unda stationara. Da noi ii vom spune tot long wire. Asa vrem noi, na!

Tavi, nu confund firul rezonant cu firul acordat. Acordul la fir evita rezonantele pina la punctul de alimentare(fed point), pe cind firul acordat le provoaca dupa fed point. Long wire-rul necesita acordul, dar evita rezonantele. E nerezonant, o zice Balanis.

In loc de epilog:
Vreau sa se inteleaga asa cum zice Tavi ca aceste aspecte legate de antene au fost studiate si intelese de cei mai buni din domeniu. O dezbatere nu poate fi benefica decit pentru aceia printre care ma consider si eu, care, avem inca de invatat. O parere a cuiva mai mult sau mai putin documentata nu are cum sa ne faca mai confuzi mai ales daca ne determina, sa ne punem mereu intrebari. Nu e nimic rau sau gresit atunci cind cauti raspunsuri. Amatorismul poate fiinta si fara practica si fara experiment, dar niciodata in lipsa pasiunii.
Cred ca am multe de invatat de la tine Tavi si de la altii de pe aici.

Pasiunea e singura scuza. Cine nu munceste nu greseste, dar nici nu iubeste - 73! Nicu

Postat de Nicu - YO5OUC la 2014-06-11 18:49:54 (ora Romaniei)
Iata ce parere are un radioamator de exceptie (G3BDQ) un practician din cap pina in picioare ce toata viata lui a construit si a masurat antene pentru radioamatori, in cartea sa "Antene Filare Practice". Cartea a fost tradusa si in limba romana si publicata de FServices SRL in 2005. In aceasta carte sunt numai antene realizate practic de catre autorul ei. Traducerea apartine radioamatorilor YO4BBH si YO3AH:

John Heys - G3BDQ zice:
"Cu mulţi ani În urmă autorul a demonstrat practic atenuarea puterii de-a lungul antenei "fir lung", L.H.THOMAS, G6QB, a instalat o antenă cu adevărat "fir lung", de 610 m, Împrejurul terenului său de golf, la Înălţimea medie de 6 m. Cu un beculeţ de neon fixat În vârful unui băţ de bambus s-a mers de-a lungul antenei observând maximele de tensiune. Pe la jumătatea antenei beculeţul abia se mai aprindea, iar la capătul ei tensiunea RF era atât de mică Încât se putea pune mâna. Punând la pământ capătul liber al acestei antene performanţele au rămas aceleaşi!"

Cit de bime se potrivesc uneori teoria cu practica. 73! de Nicu YO5OUC

Postat de Gheorghe Oproescu - Tavi - YO4BKM (yo4bkm) la 2014-06-11 20:19:08 (ora Romaniei)
@Nicu, YO5OUC, ai înţeles ce scrie un străin într-o carte tredusă şi nu ai înţeles ce am scris eu, puţin mai sus? Te rog să revezi, citez: "Postat de Gheorghe Oproescu - Tavi YO4BKM la 2014-06-08 15:57:22 (ora Romaniei) de la adresa ***.***.***.2
Nicu, YO5OUC, sunt de acord pana la un punct. Anume ca longul sa fie atat de lung incat, datorita pierderii de energie prin radiatie, cu mult inainte de capatul izolat sa nu mai existe curent prin fir si nici noduri sau ventre". Este exact ce spune şi Balanis, dar daca străinul este mai bun decat romanul chiar cand afirmă acelasi lucru este ceva specific doar românilor şi se vede cât bine ne face! Dar recunosc că în deceniile în care am folosit longul nu am ajuns cu el la o lungime de peste 42 de metri, deşi am măsurat şi eu lungimi de undă cu beculeţul cu neon în UUS pe nişte linii Lecher lungi de 3 m. Acum îmi dau seama că nemţii sunt mai încuiaţi chiar decât noi din moment ce dezvoltă în cărţile lor de referinţă antene "Langdraht" (asta înseamnă "sârmă lungă"), la care "Drahtlaenge des Strahlers groesser als eine Betriebswellenlaenge ist",adică "lungimea radiantului este mai mare decât lungimea de undă de lucru" şi "wird mit ihren Oberwellen erregt", adică se excită pe armonicele sale. Mai departe citez direct în româneşte: după modul de alimentare îşi schimbă numele în antena L, V, Fuchs, DL7AB, romb deschis etc. Dar toate se supun aceloraşi legi". Dragă Nicu, îţi recomand să-ţi concentrezi efortul asupra corectării nemţilor că ei, cu puterea lor în lume, ar putea să facă mult rău când sunt în eroare. În neştiinţa lor merg cu longul până la 8 semiunde (ruşine îmi este că am lucrat şi eu cu longul meu de 42 de m pe 28 MHz, trecând de cei 10---14 MHz fatali), mă doare sufletul să-i văd atât de neajutoraţi. Îţi doresc cât mai mult succes!

Postat de Gheorghe Oproescu - Tavi - YO4BKM (yo4bkm) la 2014-06-11 21:01:14 (ora Romaniei)
Mai am o micuţă completare: şi eu am pus mâna deseori pe radiofrecvenţa cu un nivel de 80W şi 700---1200 V (lucram cu tuburi), de la 3,5 MHz la 144 MHz, fără ca aceasta să fie atenuată, puneam mâna direct pe armăturile calde ale condensatorilor din filtrul PI. Te informez că nu este nicio scofală, radiofrecvenţa nu produce efecte fiziologice precum la 50 Hz, ce am simţit erau doar ceva efecte termice când suprafaţa de contact de pe mână era prea mică, densitatea de curent ardea pielea şi, dacă ţineam contactul prea mult, începea să mă frigă. Când lucram cu longul la cei 80 W, dacă luam un ac de cusut şi înţepam cu vârful lui în calorifer, după nici o secundă trebuia să-l arunc, atât de tare mă frigea scurgerea spre pământ a curentului captat de mine care trecea prin contactul cu acul subţire, o densitate de curent foarte mare. Am făcut multe experimente cu antene de peste 10 tipuri şi la niciuna nu am constatat pierderea energiei la capătul liber, recunosc că nu am ajuns la 610 m lungime pentru că, în pragmatismul meu, nu m-a interesat. Sincer, ai câştigat ceva lucrând cu antene mai lungi de 80 de metri? Asta mă interesează cel mai mult! În schimb mi-a plăcut pragmatismul de genul lui Edison. Edison i-a dat unui angajat al său să afle volumul unui bec. Angajatul a început să măsoare, să calculeze, Edison a umplut becul cu apă apoi a turnat-o într-un cilindru gradat. Şi nu se putea zice că nu ştia să calculeze volume la calote sferice sau trunchiuri de con. În ce mă priveşte, nimic nu poate şterge experienţa dobândită în peste 45 de ani de practică autorizată în radio.

Postat de Nicu - YO5OUC la 2014-06-11 22:34:15 (ora Romaniei)
Na ca le-am facut-o! Asa cred ca zice acum N2YO ca numai el e de vina. Vad ca mesajul tau a ajuns trunchiat si noi vorbeam de fapt de acelasi lucru. Vezi, e suficient sa te cenzureze pe ici pe colo si iasa altceva. De fapt tu ai scris sa stearga mesajul da eu, ca ardeleanu "moale din fire" ...
Imi cer scuze Tavi si ai respectele mele asa cum ti-am scris pentru ceea ce faci si ceea ce stii. De la cei ce nu au inteles nimic din ce am dezbvatut noi doi aici, dezbatere ce s-a extins si pe e-mail, imi cer scuze si rog sa nu creada ca unul dintre noi a avut dreptate si celalalt nu, ci, mai degraba ca s-a vorbit de aelasi lucru din doua perspective diferite. Noroc ca nu au mai ajuns pe aici si deductiile si demonstratiile matematice schimbate de noi prin e-mail ca ne dadeau afara de pe site.

Deci iata de fapt si concluzia:
Un long wire lucreaza nerezonant daca e foarte lung si daca puterea injectata nu e prea mare in raport cu lungimea sa. Daca lucrezi cu puteri mai mari vei observa aparitia rezonantelor. Poate lucra rezonant sau nerezonant. In general lucreaza rezonant la frecvente la limita de jos a benzii si nerezonant in benzile superioare. Conform cu teoria se vrea a fi nerezonant, dar poate fi folosit in conditii de rezonanta la fel de bine daca faci acordul din filtru pi sau transmach. La capatul de sus al benzii se acorda mai usor fiind nerezonant, iar in benziile inferioare mai greu. 73 de Nicu YO5OUC

Postat de Niculet Aurel - YO4RSS la 2014-06-17 12:11:22 (ora Romaniei)
Tavi,s-ar putea sa fi foarte bun, in astfel de articole(s-ar putea, sa fie si altii, interni sau externi).ORICUM ,articolul ,e bun.MULTUMIM.73 NICK,

Postat de Gheorghe Oproescu - Tavi - YO4BKM (yo4bkm) la 2014-06-18 08:01:35 (ora Romaniei)
TNX Nick, nu pretind ca eu sunt cel mai bun si apreciez orice contributie adusa cunoasterii in domeniul nostru. GL, 73! Tavi

Opiniile exprimate în articole pe acest site aparţin autorilor şi nu reflectă neapărat punctul de vedere al redacţiei.

Nume utilizator (forum)
Parola (forum)
Retine parola:

Nu aveti cont?	Ati uitat parola?
Pagina alternativa pentru logare!
Atentie, dupa 5 incercari nereusite de autentificare, contul se blocheaza. Puteti debloca contul de acces AICI Probleme? Vizitati pagina FAQ!