|
|
|
ÎNCĂLZIREA LINILOR DE ALIMENTAREGheorghe Oproescu - Tavi YO4BKM
ÎNCĂLZIREA
LINILOR DE ALIMENTARE Gheorghe Oproescu – Tavi
YO4BKM Subiectul a apărut din întâmplare, la o discuție cu
amicul Dan YO9CWY despre liniile de alimentare și pierderile din ele. Am
găsit că problema merită să fie analizată, chiar
dacă (uneori) producatorii (serioși) de linii de alimentare
indică puterea maximă transferată de la emițător la
antenă, dar fără detalii privind condițiile de lucru. Așa
că am continuat colaboarrea, primind multe sugestii și
observații, TNX! Pentru că între linie și antenă apar și
neadaptări care duc la apariția reflectatelor a căror putere
trebuie luată în seamă cel puțin pentru faptul că,
dacă s-ar produce între etajul final și linie, ele se manifestă
atât de evident încât provoacă distrugeri costisitoare în
emițător. Este adevărat că o linie de alimentare
este mai ieftină decât un etaj final, dar deteriorarea ei nu este atât de
ușor vizibilă în fazele de început care, continuând, generează o
avalanșă de neplăceri, mai ales dacă apar într-un concurs
într-o vară fierbinte. Linia de alimentare se încălzește deoarece o parte
din energia transportată se disipă ireversibil sub formă de
căldură pe propria rezistență electrică. Pentru
curenții de radiofrecvență fenomenul de încălzire este
amplificat și de faptul că aceștia nu trec prin toata
secțiunea conductorului ci printr-un strat aflat la suprafața lui, a
cărui grosime scade cu frecvența. Curenții de
radiofrecvență produc și încălzirea dielectricului
(izolației) dintre conductori. Linia de alimentare se află într-un
mediu cu care face schimb de căldură. La o diferență de temperatură
pană la maxim câteva sute de grade Celsius schimbul de căldură
se face preponderent prin conducție în interiorul liniei și prin
convecție în exteriorul ei, radiația termică este
neglijabilă iar linia de alimentare ajunge, în condițiile concrete de
exploatare, la o temperatură determinată de echilibrul dintre
căldura generată de sursă (efectul termic al curentului prin
conductorii liniei și pierderile prin dielectric) și căldura
schimbată cu mediul. Această temperatură se poate determina
destul de precis cu prețul folosirii unui aparat matematic prea complicat
și prea „stufos” ca să poată fi descris aici. Și pentru
că nu am găsit un model „la cheie” (nici nu mă dau în vânt
după astfel de modele după o experiență nu prea
plăcută pe acest tărâm) am construit un model fizico-matematic
completat cu constantele electrice și termice ale materialelor din linie,
am rezolvat ecuațiile căldurii și am obținut niște rezultate
pe care le voi prezenta, nu înainte de a arăta și cum am procedat. Producătorii liniilor de alimentare indică (atunci
când o fac) puterea maximă suportată de linie în cazuri normale de
utilizare, când prin ea trece doar curentul de alimentare, fără
să apară reflexii, adesea fără să precizeze alte
detalii dintre care lungimea liniei este unul din ele. Așadar linia de alimentare se încălzește de
la două surse: -
Rezistivitatea conductorilor și pierderile din dielectric; -
Undele reflectate de antenă a căror energie se disipă pe
linie. Dacă puterea specifică disipată pe linie (W/m)
este constantă în cazul rezistivității și pierderilor din
dielectric deoarece acestea sunt direct proporționale cu lungimea liniei,
încărcarea specifică în cazul reflectatelor crește odată cu
scurtarea liniei din două motive: -
Ele depind numai de adaptarea liniei cu antena, indiferent cât este
lungimea liniei; -
La liniile scurte puterea ajunsă la antenă este mai mare
deoarece se pierde mai puțin iar reflectatele reprezintă o
fracțiune din puterea care ajunge la antenă. 1. Schema de calcul și rezultatele ei la cablurile
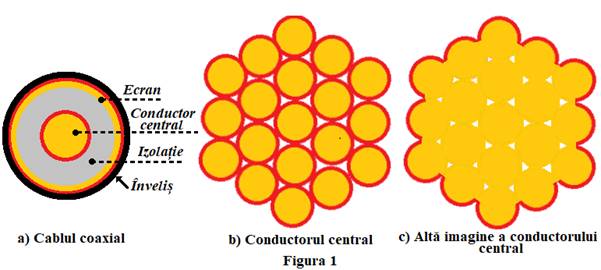
coaxiale. Inima cablului coaxial poate fi monofilară sau
multifilară. Dacă este multifilară, în jurul unui fir central se
pot dispune fie 6 alte fire (inimă cu 7 fire), fie un strat cu 6 fire apoi
un alt strat cu 12 fire (inimă cu 19 fire), cum este arătat în figura
1. Se poate vedea ușor că la 7 fire diametrul cercului
înfășurător al inimii este de trei ori diametrul firului, la 19
fire acest diametru este de cinci ori diametrul unui fir. Dacă ar mai
apare un strat acesta ar avea 18 fire (la fiecare strat se adauga 6 fire la
numărul din stratul inferior), inima ar avea in total 37 de fire și
un diametru circumscris cât șapte diametre de fir. Adâncimea de pătrundere a radiofrecvenței în cupru
este foarte mică, la materialele cu permeabilitate magnetică mare (fier)
este chiar de sute de ori mai mică. În figura 1 b) am marcat pe fiecare
fir cu roșu stratul superficial care conduce radiofrecvența, în
figura 1a) inima și tresa au fost doar simbolizate. Pentru ca un conductor
din cupru să conducă radiofrecvența pe toată secțiunea
sa ar trebui să aibe diametrul de 0,05 mm la 2 MHz, 0,035 mm la 10 MHz,
0,025 mm la 20 MHz, 0,015 mm la 50 MHz conform [1] dar și un calcul simplu
poate arăta acest lucru. Așadar firele din cablul cercetat nu vor
putea conduce pe toată secțiunea lor. Inima multifilară are câteva avantaje: -
La secțiuni mari mai multe fire subțiri măresc
flexibilitatea cablului; -
Mai multe fire subțiri, care conduc doar printr-un strat
superficial de grosime mică opun, la aceeasi sectiune cu cea a unui singur
fir, o rezistență ohmică (disipativă) mai redusă
deoarece sunt legate în paralel. Calculul rezistenței disipative datorită efectului
pelicular se poate face fie cu formula (1) indicată de [1] în care f
este frecvența în Hz iar P este perimetrul conductorului în cm, fie cu formula (2) indicată de [2] în care f
este frecvența în MHz iar d este diametrul conductorului în cm, rezultatele
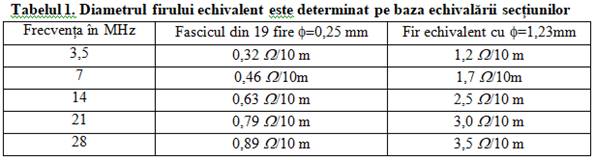
sunt identice. Dacă se folosește drept inimă un fascicul de
19 fire, fiecare fir va avea o rezistență destul de mare care, pe
ansamblul celor 19 fire legate în paralel, se reduce considerabil, tabelul 1
arată valorile comparate și nu necesită nicio discuție. Pentru modelarea încălzirii am adoptat următoarele
ipoteze: -
O primă sursă termică o formează puterea
disipată pe stratul superficial al firelor din conductorul central și
pe ecranul (tresa) considerat un conductor tubular cu strat superficial de
conducție. Evaluarea lor se poate face pe baza curenților din linie
și a rezistențelor calculate cu formulele (1) sau (2). -
A doua sursă termică o formează pierderile care apar în
dielectric. Aici formulele de calcul de găsesc mai greu și nu sunt
foarte exacte și am ales ca pierderile din dielectric să se calculeze
scăzând din pierderile calculate cu valoarea atenuării dată de
catalog, pierderile date de rezistivitate. Dar, ca să poată fi
posibil acest lucru trebuie găsită o relație de
interpolare-extrapolare pe un domeniu larg de frecvențe a atenuărilor
pe care cataloagele le dau doar pentru câteva frecvențe, adesea peste 50
--- 100 MHz până la cîteva mii de MHz. -
A treia sursă termică o formează puterea undelor
reflectate, ușor de calculat cunoscând SWR între linie și
antenă. în care -
Datorită conductibilității termice ridicate a cuprului,
dimensiunilor mici ale firelor și contactului intim între ele, închise
într-un volum foarte mic, am considerat sursa diseminată în toată
secțiunea conductorului central și a ecranului (tresei), dar numai
pentru calculul termic. -
Mediul înconjurător realizează o convecție liberă la
temperatura aerului și poate fi setat ca aer calm, vânt moderat sau vânt
puternic. Am început modelarea cablului H155 (pe care îl folosesc în
prezent), puterea transmisă de 100 W, situat în aer calm la 20 0Celsius.
La acest cablu am găsit [5] (tnx YO9CWY) ca date de catalog atenuarile
(dB/100m) pentru 12 frecvente de la 10 MHz la 2050 MHz. Cu acestea am
căutat o formulă pentru interpolarea-extrapolarea datelor de catalog alegând
o dependență politropică funcție de frecvență
(4), de care mă convinsesem în mai multe rânduri că răspunde
destul de bine la modelarea funcțiilor cu alura necunoscută și care
să fie folosită pe domeniul care ne interesează pe noi (1,8
MHz---1296 MHz) și în care coeficienții se determină prin
metode folosite [3], după care am pus la punct softul pentru modelarea
câmpului termic din cablu, atât în regim dinamic cât și stabilizat, de
fapt reluând o experiență de acum cca 20 de ani când modelam
regimurile termice în conductele care trebuiau să transporte lichide în
medii cu temperaturi scăzute până la -25 grade Celsius. Am avut
impresia că totul merge bine pentrtu H155, formula (4) verifica foarte
bine datele din catalog dar, când am trecut la cercetarea cablului RG6 am
costatat că ceva nu se potrivește. Deși valorile date de
formulă coincideau și la RG6 destul de bine în punctele date în
catalog, când am scăzut din aceste valori pe cele calculate ca disipare
rezistivă ca să pot afla și disiparea în dielectric, puterea
disipată pe dielectric rezulta negativă, deci în loc de
încălzire produceau răcire. A fost nevoie sa reiau de la capăt modelul pierderilor
și am constatat că chiar o eroare acceptabilă, de 5%-8% la
interpolarea-extrapolarea datelor de catalog, era prea mare, mai ales la
frecvențe reduse unde pierderile din dielectric sunt destul de mici.
Problema apărea deoarece cele două componente ale atenuării pe
ansamblul cablului depind în mod diferit de frecvență iar
frecvența cuprinde un domeniu de valori foarte larg, într-un raport de
câteva mii, de la 1,8 MHz la 5 GHz. Pe de altă parte atenuările din
cupru calculate pe baza rezistenței stratului superficial, cum am
arătat mai sus, rezultau prea mari deoarece la un fascicul de fire,
datorită contactului intim între ele, stratul de conducție nu mai
înconjoară fiecare fir ci se dispune numai pe arcele exterioare între
punctele în care firele fac contact între ele, deoarece numai acestea formează
„suprafața” fasciculului, figura 1 c). Diametrul unui fascicul cu 19 fire
este de 5 ori mai mare decât al unui singur fir, perimetrul este cu mult mai
mare din cauza ondulațiilor (figura 1c) iar rezistența sa
electrică conform (1) sau (2) va scădea de cel puțin 5 ori.
Chiar și un fascicul de 7 fire are perimetrul de cel puțin 3 ori mai
mare decât al unui fir, deci o rezistență de cel puțin 3 ori mai
redusă. Mai apare și faptul că la RG6 tresa este din doua
straturi, așa cum este la multe alte cabluri, deci se depărtează
de ipoteza unui conductor tubular pur. Astfel am ales să evit calculul
puterii disipate în cupru datorită acestor aspecte greu de prins într-o
relație exactă și, deși perimetrul unui fascicul de fire
(figura 1 c) nu este greu de calculat, am încercat abordarea problemei
căutând mai întâi o relație pentru disiparea pe dielectric. Cu
puțin noroc (pe care se zice că și-l face și omul cu mâna
lui) am găsit în [1] și în [4] că atenuarea din dielectric se
poate exprima cu formula (5), corectată pentru unitățile de
măsură uzuale azi: unde f este frecvența în Hz, c este
viteza undei în dielectric în m/s, d
este unghiul de pierderi. Dacă formula (5) este foarte simplă, nu
este la fel de simplu de aflat cât este tg(d), cele mai „exacte” valori pentru polietilenă (PE) le
dă tot [4], tg(d)=0,0004---0,0009.
Combinând și cu alte surse am ales tg(d)=0,0007. Deoarece atenuarea din dielectric se află acum
mai ușor, atenuarea din cupru va rezulta prin diferență
față de valorile calculate, mai ales din cauza indentificării
imprecise a stratului superficial deoarece nu se știe sigur cum se face
contactul dintre fire.. Iar formula de interpolare-extrapolare a valorilor din
catalog va fi mai simplă, unde f este în Hz iar a1 și a2 rezultă prin
minimizarea abaterii medii pătratice dintre valorile calculate și
cele din catalog printr-un algoritm Gauss [3] programat de mine în mediul Lazarus.
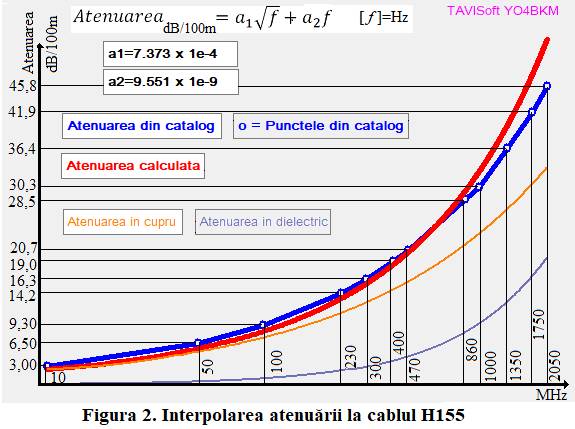
Pentru cablul H155 rezultatele sunt arătate în figura2 Precizez că în figura 2 scara frecvențelor este
logaritmică deoarece ecartul mare (de peste 200 de ori) ar fi „înghesuit”
frecvențele mici. În formula (6) frecvența este în
unitățile sale naturale, am folosit logaritmarea numai pentru
reprezentarea grafică. Din acest motiv atenuarea din dielectric, care ar
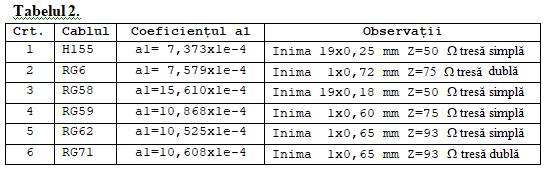
fi trebuit să fie liniară, apare sub forma unei linii curbe. Pentru alte cabluri coeficienții formulei (6) sunt
dați în tabelul 2. Deoarece cablurile au izolația din PE al doilea
termen din formulă este același la toate. Dar calculul termic, care
se prezintă în continuare, ține cont de
dimensiunile cablului (diametre, lungimi), inclusiv pentru dielectric. Pentru calculul termic am folosit ecuațiile
căldurii ale lui Fourier ( [3], același cu seria și transformata
care-i poartă numele) în care sunt cunoscute puterea dispiată pe
componentele cablului (cupru și dielectric în W/m.c), dimensiunile
componentelor și constantele fizice ale acestora precum conductibilitatea
termică în W/(mK), căldura specifică în J/(kgK), densitatea în
kg/m.c și coeficientul de convecție în W/(m.p.K), programate în
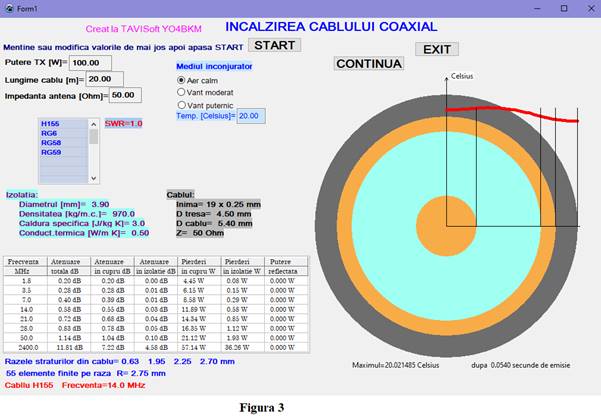
același mediu, Lazarus, în care lucrez astfel de probleme. În figura 3
arăt pagina ecran a aplicației la un anumit moment. Secțiunea cablului a fost împărțită în
elemente finite cu valoarea de 0,05 mm pentru care, pentru a obține
stabilitatea soluției în regim dinamic, a trebuit să aleg incrementul
de timp la valori mai mici de 0,0000004 secunde, dacă aș fi
mărit valoarea acestuia rezolvarea devenea instabilă după câteva
iterări. Asta înseamnă că pentru fiecare element finit sunt
necesare 1/ 0,0000004=2500000 calcule pentru a afla ce se întâmplă
după o secundă de funcționare, pentru toate elementele finite
sunt necesare sute de milioane de calcule doar pentru o secundă de emisie.
Pentru un regim dinamic de câteva zeci de secunde se fac miliarde de calcule,
pe calculatorul meu acestea dureaza maxim 10---20 de secunde până la
stabilizarea regimului termic. Micșorarea elementului finit ar fi dus la o
scădere și mai drastică a incrementului de timp și lungirea
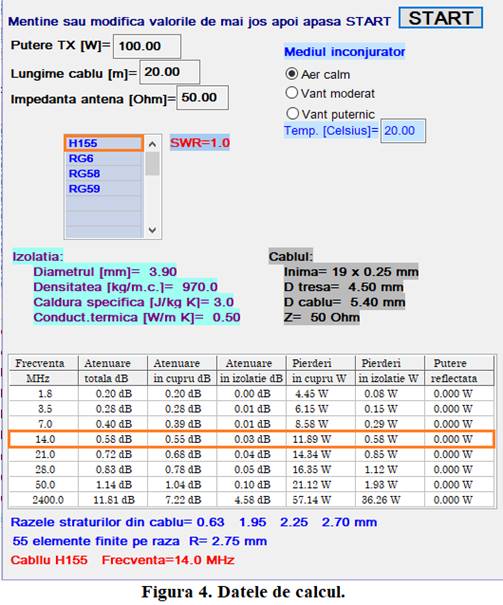
exagerată a calculului. Pentru că pagina ecran apare prea mică în pagina
articolului și cu detalii greu lizibile, voi arăta în continuare doar
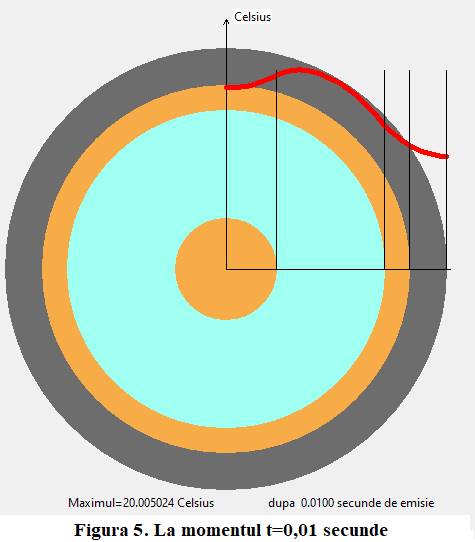
detalii din ea, figura 4 arată cu ce valori am setat calculul termic. În figura 5, care arată partea dreaptă a
ecranului, se vede regimul termic după 0,01 secunde de emisie. Dielectricul
este mai cald decât mediul înconjurător (cu câteva miimi de grade Celsius)
datorită disipării mai dificile a căldurii atât produse în el cât
și primită de la inima cablului, tresa se răcește mai
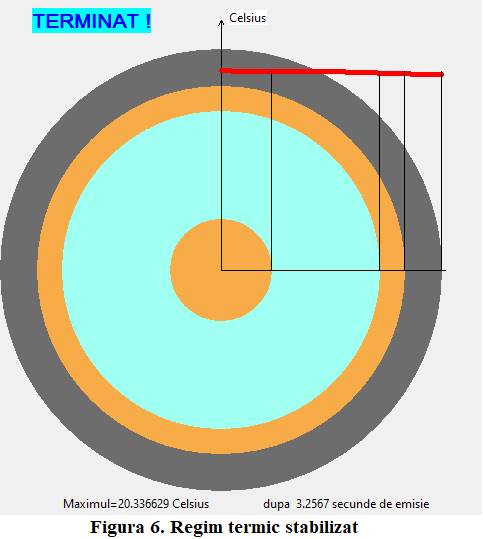
ușor prin mantaua exterioară. Stabilizarea termică apare la momentul t=3,25 secunde
de emisie și se vede în figura 6. O încălzire nesemnificativă
și un camp termic aproape constant pe secțiune. O supraîncălzire
de 0,33 grade Celsius pentru o putere de cca 12,5 W disipată pe cablul
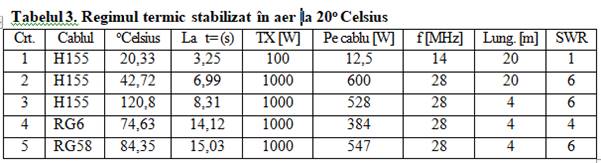
lung de 20 m, revenind așadar cca 6 mW/cm lungime. Procedând la fel și pentru alte cazuri, rezultatele se
prezintă în tabelul 3. Am considerat că antena are impedanța de
alimentare de 50 W la cazul 1 și
300 W la celelalte. La cazul 3 cablul
nu rezistă din „vina” reflectatelor. La valorile din tabelul 3 trebuie adăugată și
diferența dintre temperatura mediului și cele 20 grade Celsius la
care au fost deduse datele din tabel. De exemplu vara, în soare, cablul poate
să se încălzească de la mediu la temperaturi de 40 --- 60o
Celsius, cazurile 4 și 5 putând duce la deterioarea sa. 2. Concluzii. Modelul dezvoltat nu a fost comparat cu niciun experiment, din
acest motiv sunt convins că valorile calculate nu sunt dintre cele mai
corecte, în mod obișnuit orice modelare numerică (instrumentație
virtuală) se bazează pe cel puțin un caz cercetat experimental
iar diferențele dintre rezultatele teoretice și experimentale servesc
la ce se numește „acordarea modelului”. Sunt convins însă că
discuțiile pe această temă vor fi folositoare. Cu toate acestea,
se pot desprinde câteva concluzii: -
Cablul coaxial se încălzește proporțional cu
frecvența la care lucrează, considerând ca sursă termică
pierderile prin rezistența mediilor conductoare și prin dielectric; -
Pierderile prin rezistivitatea conductorilor depind direct
proporțional cu rădăcina pătrată a frecvenței de
lucru, pe când pierderile în dielectric depind direct proporțional cu
frecvența. Asta face ca la frecvențe joase să domine pierderile
prin rezistivitate iar la frecvențe înalte să domine pierderile în
dielectric. -
Fără unde reflectate încălzirea cablului nu depinde de
lungimea sa deoarece puterea care se transform în căldură este, la
aceeași frecvență, proporțională cu lungimea, așa
cum este și răcirea cablului, raportul dintre căldura
cedată și disipirea ei în mediu rămâne constant. Dacă apar
unde reflectate încălzirea crește invers proporțional cu
lungimea cablului; -
Cablurile scurte sau / și cu pierderi mici dar neadaptate cu antena
se încălzesc mult mai mult deoarece puterea undelor reflectate de
antenă este mai mare (se pierde mai putin pe cablu) și se
concentrează într-un volum mai mic al cablului. 3. O
metodă simplificată de evaluare a încălzirii În cazul neadaptării liniei la antenă exista o
cale mai rapidă (dar mai puțin precisă) de a afla dacă
linia de alimentare poate suporta anumite încărcări energetice. Din
tabelul 3 se vede că disiparea rezistivă nu este atât de
periculoasă ca în cazul neadaptării cu antena. O verificare simplă, cu datele din tabelul 3 pentru
cazul 3 (cea mai mare incălzire), poate arăta astfel: alegem un rezistor
de putere care are diametrul cât mai apropiat de al cablului
coaxial și, să zicem, că acesta are o lungime de 2,3 cm.
Calculăm cât din cei 528 W/(4m) disipați pe cablu revin pe 2,3
cm, rezultă 528/400 x 2,3=3,036 W/(2,3cm). Pentru că rezistorul nu
conține polietilenă și poate suporta temperaturi mai mari, consider
că se poate avea încredere în metoda simplificată dacă
rezistorul ales pentru comparație disipă o putere de 2-3 ori mai mare.
Dacă rezistorul disipă o putere de 6---9 W putem aprecia că
și cablul va suporta puterea undelor reflectate. Bibliografie. [1] B.A. Smirenin, Manual de radiotehnică, vol
1, Traducere din limba rusă, Editura Energetică de Stat,
1953. [2] Karl Rothammel DM2ABK, Antennenbuch, Detscher Militärverlag,
1968. [3] Oprescu
Gheorghe, Metode numerice și aplicații, EDITURA TEHNICA–INFO
CHISINAU 2005. [4] Sophocles J. Orfanidis, Electromagnetic Waves
and Antennas. www.ece.rutgers.edu/~orfanidi/ewa [5] *** https://www.scribd.com/document/411646317/PDF-RG-coaxial-Cables-Helukabel
Articol aparut la 31-10-2021 2581 Inapoi la inceputul articolului | |
|
Comentariul trebuie sa se refere la continutul articolului. Mesajele anonime, cele scrise sub falsa identitate, precum si cele care contin (fara a se limita la) atac la persoana, injurii, jigniri, expresii obscene vor fi sterse iar dupa caz se va ridica dreptul de a posta comentarii.
| |||||
Opiniile exprimate în articole pe acest site aparţin autorilor şi nu reflectă neapărat punctul de vedere al redacţiei.
|
Copyright © Radioamator.ro. Toate drepturile rezervate. All rights reserved
Articole | Concursuri | Mica Publicitate | Forum YO | Pagini YO | Call Book | Diverse | Regulamentul portalului | Contact |
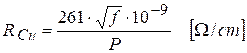 (1)
(1)
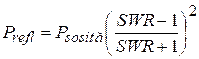 (3)
(3)